В тетради записать номера утверждений и отметить: знаком « + » верные утверждения,
знаком « - » неверные утверждения.
1) Начальные геометрические сведения
(отрезки, прямые и углы).
1. Существуют три прямые, которые проходят через одну точку.
2. Смежные углы всегда равны.
3. Вертикальные углы равны.
4. Всегда один из двух смежных углов острый, а другой тупой.
5. Через заданную точку плоскости можно провести только одну прямую.
6. Если угол острый, то смежный с ним угол также является острым.
7. Через две различные точки на плоскости проходит единственная прямая.
8. Сумма смежных углов равна 180°.
2) Параллельные и перпендикулярные прямые.
1. Две прямые, параллельные третьей прямой, перпендикулярны.
2. Две прямые, перпендикулярные третьей прямой, перпендикулярны.
3. Две различные прямые, перпендикулярные третьей прямой, параллельны.
4. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
5. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
6. Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
7. Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
8. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти две прямые параллельны.
9. Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
10. Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то эти две прямые параллельны.
11. Если при пересечении двух прямых третьей прямой сумма внутренних односторонних углов равны 180°, то эти две прямые параллельны.
3) Треугольник.
1. Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
2. В любом тупоугольном треугольнике есть острый угол.
3. В тупоугольном треугольнике все углы тупые.
4. В треугольнике против большего угла лежит большая сторона.
5. Внешний угол треугольника больше не смежного с ним внутреннего угла.
6. Внешний угол треугольника равен сумме его внутренних углов.
7. Медиана треугольника делит пополам угол, из вершины которого проведена.
8. Один из углов треугольника всегда не превышает 60 градусов.
9. Сумма углов любого треугольника равна 360 градусам.
10. Треугольник со сторонами 1, 2, 4 существует.
13. Биссектриса треугольника делит пополам сторону, к которой проведена.
14. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
15. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
16. Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
17. Всякий равнобедренный треугольник является остроугольным.
18. Каждая из биссектрис равнобедренного треугольника является его высотой.
19. Каждая из биссектрис равнобедренного треугольника является его медианой.
20. Сумма углов равнобедренного треугольника равна 180 градусам.
21. Все высоты равностороннего треугольника равны.
22. Всякий равносторонний треугольник является равнобедренным.
23. Всякий равносторонний треугольник является остроугольным.
24. В прямоугольном треугольнике гипотенуза равна сумме катетов.
25. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
26. Сумма углов прямоугольного треугольника равна 90 градусам.
27. Сумма острых углов прямоугольного треугольника равна 90 градусам.
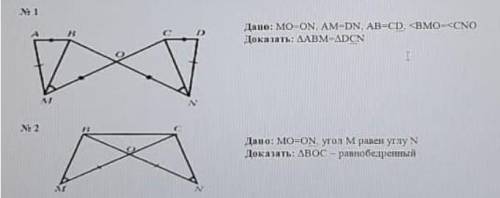
(Сделай лучшим)
(Рисунок к задаче 8)
6) Дано:
Трикутник ABC
Кут BAZ = 150° (точка z - за межею завершенного відрізка CA)
Кут ACB = 110°
x - ?
Розв'язання:
Кут CAB, за властивістю суміжних кутів (сума суміжних кутів дорівнює 180°) дорівнює 180°-150°=30°. Сума всіх кутів трикутника дорівнює 180°. 180-110-30=40° (кут ABC). Знову використовуємо властивість суміжних кутів. 180-40=140° = x
Відповідь: x = 140°
7) Дано:
Трикутник ABC
Вертикальний кут до кута CAB = 62°
Кут ABC = 80°
x - ?
Розв'язання:
Кут, що даний і дорівнює 62° вертикальний до кута CAB, а оскільки вертикальні кути дорівнюють один одному - кут CAB дорівнює 62°. Сума всіх кутів трикутника дорівнює 180°. Кут BCA дорівнює 180°-80°-62°=38°. Оскільки вертикальні кути дорівнюють один одному то кут вертикальний до кута BCA дорівнює йому. Їх сума - 76°. Коло - 360°. x = (360-76)/2=142°
Відповідь: x = 142°
8) Дано:
Трикутник ABC (Кут B = 90°)
Кут A - Кут C = 22°
Кут C - ?
Розв'язання:
Сума всіх кутів трикутника дорівнює 180°. Сума двох гострих кутів прямокутного трикутника дорівнює 90°.
90° = x + x +22°.
68°=2x
34°=x=Кут С
Відповідь: Кут С (менший з гострих кутів трикутника) дорівнює 34°