Объяснение:
1. находим боковые стороны равнобедренного треугольника через его площадь:
S=a²sin120°/2 ⇒ a²=(25√3)/(√3/2)/2=25*4, a=√(25*4)=5*2=10 см - боковые стороны.
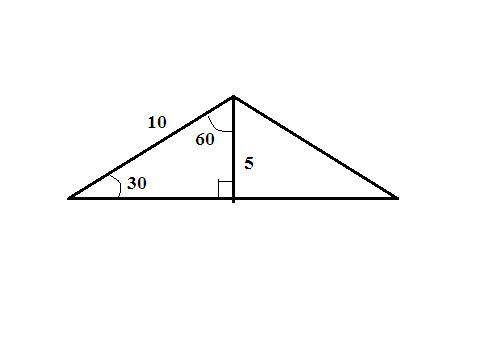
2. находим основание:
высота, проведенная к основанию равнобедренного треугольника, образует с боковой стороной и половиной основания прямоугольный треугольник где гипотенуза - боковая сторона - 10 см. Углы в этом треугольнике 90°, 60°, 30°. Против угла 30° (высота треугольника) лежит катет в два раза меньше гипотенузы ⇒ высота - 10/2=5 см;
далее либо по т. Пифагора находим половину основания треугольника, либо через формулу нахождения площади находим длину всего основания.
т. Пифагора: √(10²-5²)=√75=5√3 см - половина основания, (5√3)*2=10√3 - основание треугольника;
через площадь: в*h/2=25√3, в=50√3/5=10√3 см.
О - точка пересечения биссектрис треугольника АВС.
∠AOB = ∠COB. Найти наименьший угол треугольника ABC, если ∠ABC в три раза меньше ∠AOC
ответ: 36°
Объяснение:
ВО- биссектриса угла В, ∠AOB =∠COB (дано)⇒
∆ АОВ=∆ СОВ по двум углам при общей стороне ВО ( 2-й признак). ⇒
∠ВОА=∠ВОС.
Т.к. АО и СО - биссектрисы, то и ∠ВАС=∠ВСА. как состоящие из равных половинок. ⇒ ∆ АВС равнобедренный.
Примем ∠ОАС и ∠ОСА равными α. Тогда ∠АОС=180°-2α.
∠АВС=180°-4 α.
Составим уравнение согласно условию:
∠ АОС=3∠ АВС⇒
180°-2α=3(180°-4α). Произведя необходимые вычисления, получим 10α=360°⇒ α=36°
Угол АВС=180°-4•36°=36°.
Углы А и С вдвое больше α, они равны по 72°.
Следовательно, наименьший угол ∆ АВС - угол АВС=36°