
Основное тригонометрическое тождество:
sinα^2 +cosα^2 =1
Следовательно
sinα =+-√(1-cosα^2)
Синус угла от 0 до 180 - положительный
sinα =√(1 -9/10) =√(1/10)
tgα =sinα/cosα =1/√10 : 3/√10 =1/3
Или (то же самое)
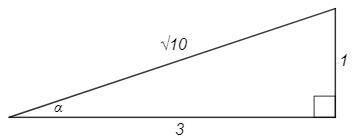
Косинус острого угла в прямоугольном треугольнике - отношение прилежащего катета (b) к гипотенузе (c).
Тангенс острого угла в прямоугольном треугольнике - отношение противолежащего катета (a) к прилежащему (b).
cosα=3/√10 =b/c
Пусть b=3, c=√10
По теореме Пифагора
a^2 +b^2 =c^2 => a =√(c^2 -b^2) =√(10-9) =1
tgα =a/b =1/3
Треугольники DKN и MNC подобны, то есть MN/NK = CM/DK; точно также из подобия треугольников EKN и ANM получается MN/NK = AM/KE; если обозначить
MN/NK = x; то CM = DK*x; AM = KE*x;
то есть CM/AM = DK/KE; (1)
Далее, поскольку DE II AB, то треугольники DKB и AMB подобны, и DK/AM = BK/BM; точно так же из подобия треугольников BKE и BMC следует KE/CM = BK/BM; если обозначить BK/BM = y; то DK = AM*y; KE = CM*y;
то есть CM/AM = KE/DK; (2)
Если перемножить равенства (1) и (2), получится (CM/AM)^2 = 1; то есть CM = AM; Вот так решается