1.
Т.к. площадь параллелограмма равна произведению высоты на сторону, к которой она проведена
S АВСД =АВ·ВД
АВ найдем из прямоугольного треугольника АВД
АВ= 108:9:2 =6 см
АД=√(АВ²+ВД²)=√117см
2.
Если АВ=СD
Опустим из вершины В к АД высоту h
Расстояние между вершиной угла при большем основании и точкой пересечения высоты с большим основанием в равнобедренной трапеции равно полуразности оснований.
(30-14):2=8
h=√(144-64)=√80=4 см√5
S=4√5·(30+14):2=88√5 см²
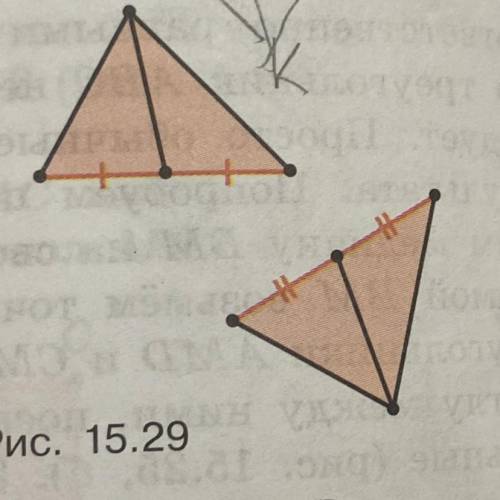
3.
В исходном Δ KMN и построенном Δ NMР вершина общая и высота у них общая. Для того, чтобы площадь треугольника NMР была в два раза меньше площади Δ KMN, основание МР в Δ NMР должно быть в два раза меньше основания КN в Δ KMN,
неизвестная площадь NKM = s;
a - s = KL*KN*sin(α)/2;
b - s = KM*KP*sin(α)/2;
если это перемножить, то
(a - s)*(b - s) = KL*KN*KM*KP*(sin(α))^2/4 = a*b*(sin(α))^2;
(a - s)*(b - s) = a*b*(sin(α))^2;
осталось решить квадратное уравнение
s^2 - (a + b)*s + a*b*(cos(α))^2 = 0;
s = (a + b)/2 +- √((a + b)^2 - a*b*(cos(α))^2);
s = (a + b)/2 +- √(a^2 + b^2)/2 + a*b*(sin(α))^2);
Осталось понять, какой оставить знак.
s = (a + b)/2 - √(a^2 + b^2)/2 + a*b*(cos(φ))^2);
я нашел частный случай, очень легкий, и по нему можно понять, что остается именно "минус". Пусть α = π/6; и сам треугольник KLM имеет угол L = π/6; оба треугольника получаются одинаковые, и их пересечение имеет площадь a/2, то есть s = (a + b)/4