Объяснение:
Дано:
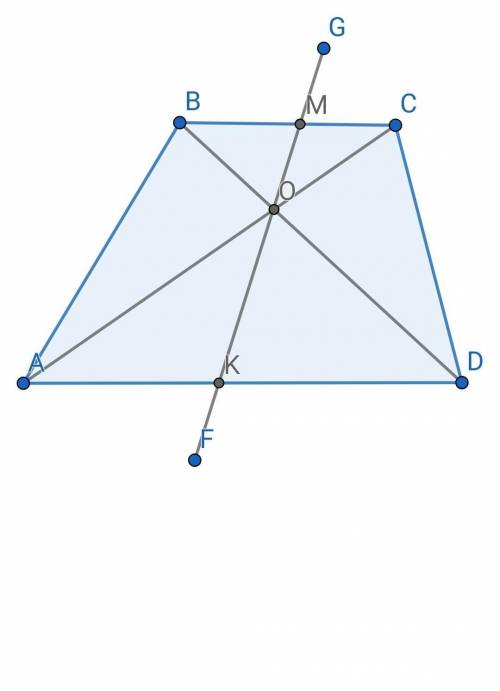
Трапеция АВСD
прямая FG
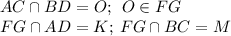
Доказать что
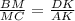
Доказательство
АВСD - трапеция => ВС || АD
Тогда диагонали АС, ВD и прямую FG можно рассматривать как секущие при 2х параллельных.
Соответственно,
- будут равны углы (как накрест лежащие):
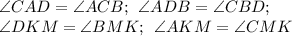
- будут равны как вертикальные:
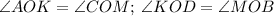
Рассм. подобные ∆-ки.
Вследствие равенства углов подобны:
∆АОК и ∆СОМ
∆DОК и ∆BОМ.
Коэффициент подобия:
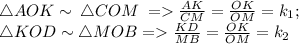
Oчевидно, что в обоих случаях коэффициент подобия можно выразить через одно и то же соотношение, а значит коэффициенты равны:
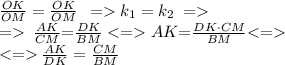
Что и требовалось доказать
Вписанный прямой угол опирается на диаметр.
ACD=90 => AD=8*2 =16 (диаметр)
Катет против угла 30 равен половине гипотенузы.
CAD=30 => CD=AD/2 =8
Равнобедренная трапеция, боковые стороны равны.
AB=CD =8
Сумма острых углов прямоугольного треугольника 90.
CDA=90-CAD =60
Равнобедренная трапеция, углы при основании равны.
BAD=CDA =60
BAC=BAD-CAD =60-30=30
Вписанный угол равен половине дуги, на которую опирается.
BAC=CAD => ∪BC=∪CD
Равные дуги опираются на равные хорды.
∪BC=∪CD => BC=CD =8
P(ABCD)=8+8+8+16 =40 (см)