66 см²
Объяснение:
Медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от вершины.
⇒ ВМ:МК=2:1.
У ΔАМК и ΔАВМ одна и та же высота АН - перпендикуляр, проведенный из вершины А к прямой ВК, содержащей стороны ВМ и МК этих треугольников.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты) ⇒
Samk/Sabm=1/2 ⇒
11/Sabm=1/2 =>
22=Sabm.
Sabk=22см²+11см²=33см²
медиана ВК делит ΔАВС на два равновеликих т.е Sabk = Skbc.
⇒
Sabc=33*2=66см²
Решение: Пусть О – центр окружности, пусть Р – ближняя из точек пересечения окружности и отрезка АО. Пусть N – точка пересечения
Тогда прямоугольные треугольники OAC и ОAB равны за катетом и гипотенузой(ОF=ОA, ОC=ОB – как радиусы).Значит из равности треугольников,AC=AB
угол АOC=угол AOB(то же самое угол РOC=угол РOB)
угол OAC=угол OAB(то же самое угол OРC=угол OРB ), значит АP – биссектриса угла А,(то же самое, что AN - биссектриса угла А )
AC=AB – значит треугольник ABC – равнобедренный
Биссектриса равнобедренного треугольника, проведенная к основанию, есть его высотой и медианой
треугольник ABC – равнобедренный, AN - биссектриса угла А, значит
угол ANB= угол ANC=90 градусов
треугольник BOP – равнобедренный (BO=OP – как радиусы),
значит угол PBO= угол BPO
Пусть угол BOA= угол BOP= угол BON=х.
Сумма углов треугольника равна 180.
Сумма острых углов прямоугольного треугольника равна 90 градусов.
Тогда с треугольника BOP
угол PBO= угол BPO=(180 -х)\2=90-х\2
с треугольника AOB угол OAB=90-х
угол ABP= угол OAB- угол PBO=90-х-(90-х\2)=x\2
угол PBN=90-угол OAB- угол ABP=90-(90-x)-x\2=x\2
угол ABP= угол PBN, значит BP – биссектриса угла B.
Итак, точка P- точка пересечения биссектрис треугольника ABC, что и требовалось доказать.
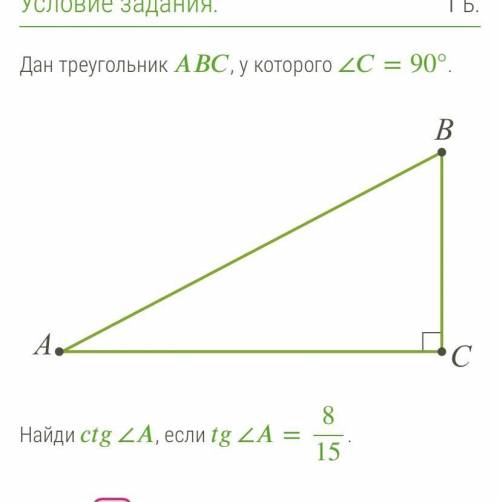
ctg∠A=15/8
Объяснение:
tg∠A*ctg∠A=1
ctg∠A=1/tg∠A
ctg∠A=1:8/15
ctg∠A=15/8