Задание 1. В прямоугольном треугольнике ВСА (∠А = 90°) ВС = 20, ∠АВС = 30°. С центром в точке
С проведена окружность. Каким должен быть ее радиус, чтобы:
а) окружность касалась прямой АС;
b) окружность не имела общих точек с прямой АС;
c) окружность имела две общие точки с прямой АС?
d) найдите диметр окружности.
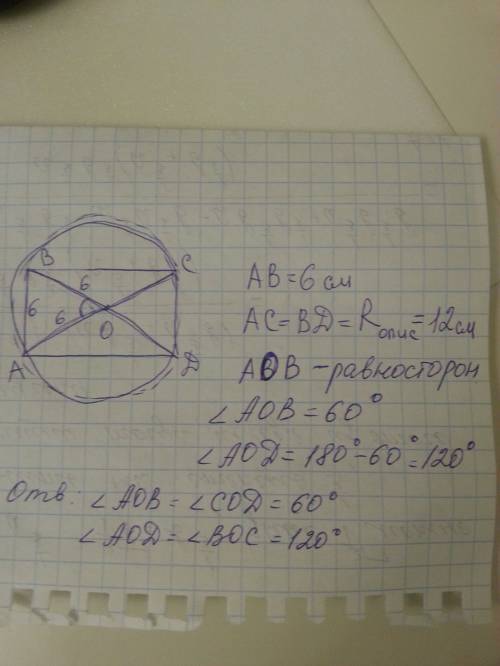



6. 60 см
7. 21,2
8. в
9. 32
Объяснение:
6. Вторая диагональ делит угол В пополам, т.е. 30+30.В прямоугольном треугольнике ВОС ОС = 15/2=7,5 и лежит против угла 30 градусов, следовательно, гипотенуза ВС=15см. А весь периметр 15х4=60см.
7. 8,4/4=21,2 дм
8. Прямоугольники.
углы В и С в сумме дают 180 град, 60+30+90, а они являются внутренними односторонними при прямых АВ и СД и секущей ВС. т.е. АВ ║СД, по признаку параллельноти прямых.
9. Пусть х-меньшая сторона, х+4-большая сторона.
2x+2(x+4)=24
4x=16,x=4-1 сторона
x+4=8-2 сторона
S=x(x+4)=4*8=32