
1) Формула объёма конуса V=S•H:3=πr²H:3
Формула объёма шара
V=4πR³:3
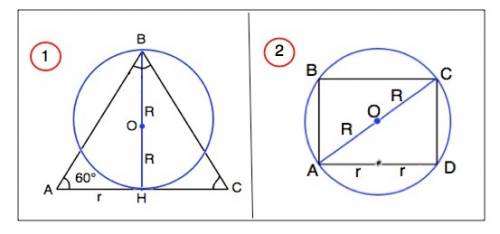
Осевое сечение данного конуса - равносторонний треугольник, т.к. его образующая составляет с плоскостью основания угол 60°.
Выразим радиус r конуса через радиус R шара.
r=2R:tg60°=2R/√3
V(кон)=π(2R/√3)²•2R²3=π8R³/9
V(шара)=4πR³/3
V(кон):V(шар)=[π8R³/9]:[4πR³/3]=(π•8R³•3/9)•4πR³=2/3
———————
2) Формула объёма цилиндра
V=πr²•H
Формула площади осевого сечения цилиндра
S=2r•H
Разделим одну формулу на другую:
(πr²•H):(2r•H)=πr/2⇒
96π:48=πr/2⇒
4π=πr
r=4
Из площади осевого сечения цилиндра:
Н=S:2r=48:8=6
На схематическом рисунке сферы с вписанным цилиндром
АВ- высота цилиндра, ВС - его диаметр,
АС - диаметр сферы.
АС=√(6²+8²)=√100=10
R=10:2=5
S(сф)=4πR8=4π•25=100π см²
ответ
3. В параллелограмме MPKT на стороне MT отмечена точка E, =∠PEM=900, ∠EPT=450, МЕ = 4 см, ЕТ = 7 см. Найдите площадь параллелограмма
4,0/5
9
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
PE перпендикулярна к MT, PE — высота.
S = MT * PE
MT = ME + ET = 4см + 7см = 11см
Рассмотрим треугольник PET. ∠PET = 90°, ∠EPT = 45°. По свойству углов в треугольнике, ∠PTE = 180° – ∠PET – ∠EPT = 180° – 90° – 45° = 45°.
∠PTE = ∠EPT = 45°, получается треугольник PET — равнобедренный, значит PE = ET = 7см.
S = MT * PE = 11см * 7см = 77см^2
думаю правильно если нет извини