Объяснение:
Задача кривая. Слишком много данных, при этом не сходятся 2 различных решения.
Решение 1:
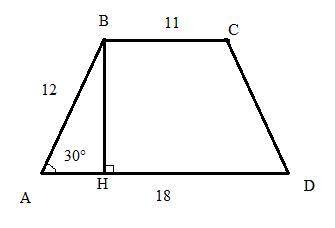
Пусть ВН - высота. Тогда в прямоугольном треугольнике △АВН ВН=(1/2)*АВ=12/2=6см (катет, лежащий против угла в 30°).
S(ABCD)=((AD+BC)/2)*BH=((18+11)/2)*6=87см².
Решение 2:
Основания высот равнобедренной трапеции, опущенных из вершин меньшего основания, делят большее основание на отрезки, один из которых равен меньшему основанию, а два других – полуразности оснований.
То есть АН=(AD-BC)/2=(18-11)/2=3,5см.
Тогда в прямоугольном треугольнике △АВН ВН=√(АВ²-АН²)=√(12²-3,5²)=√131,75см.
S(ABCD)=((AD+BC)/2)*BH=((18+11)/2)*√131,75=166,43см² (примерно)
Рекомендую конечно взять первое решение, но почему они не сходятся - понятия не имею.
CF : FD = BE : EA = 2 : 3 по теореме Фалеса
Проведем диагональ BD, О - точка пересечения диагонали и EF.
ΔЕВО подобен ΔABD по двум углам (угол В общий, ∠ВЕО = ∠ВАD как соответственные при пересечении параллельных прямых EF и AD секущей АВ),
ЕО : AD= BE : BA = 2 : 5
EO = AD · 2 / 5 = 7 · 2 / 5 = 14/5 = 2,8 см
ΔDOF подобен ΔDBC по двум углам (угол D общий, ∠DOF = ∠DBC как соответственные при пересечении параллельных прямых EF и ВС секущей BD)
OF : BC = DF : DC = 3 : 5
OF = BC · 3 / 5 = 4 · 3 / 5 = 12/5 = 2,4 см
EF = EO + OF = 2,8 + 2,4 = 5,2 см