
АВ=ВС
Высота, опущенная на основание равнобедренного треугольника, является и медианой, и биссектрисой
Следовательно, ∠ABD=∠CBD, AD=DC
ΔABD прямоугольный
Находим ∠ABD:
∠ABD=120°:2=60°
∠ВАD=180°-90°-60°=30°
Катет, лежащий против угла 30°, равен половине гипотенузы
Исходя из этого:
BD=AB:2
AB=2*BD=2*13=26 см
ответ: боковая сторона равнобедренного треугольника (AB=BC) равна 26 см
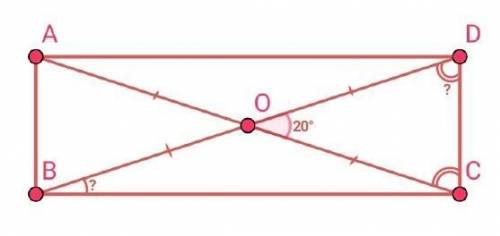
Дано :
Четырёхугольник АВСD — прямоугольник.
Отрезки BD и AC — диагонали.
Точка О — точка пересечения диагоналей.
∠DOC = 20°.
Найти :
∠BDC = ?
∠DBC = ?
Диагонали прямоугольника равны и точкой пересечения делятся пополам.Отсюда AO = OC = OD = OB.
Рассмотрим ∆ODC — равнобедренный (по определению).
Следовательно ∠ODC = ∠DCO (по свойству равнобедренного треугольника).
По теореме о сумме углов треугольника —
∠DOC + ∠ODC + ∠DCO = 180°
∠ODC + ∠DCO = 180° - ∠DOC = 180° - 20° = 160°
∠ODC = ∠DCO = 160°/2 = 80°.
Рассмотрим ∆BDC — прямоугольный.
По теореме о сумме острых углов прямоугольного треугольника —
∠BDC + ∠DBC = 90°
∠DBC = 90° - ∠BDC = 90° - 80° = 10°.
80°, 10°.
26
Объяснение:
против углов в 30 градусов лежит высота = 13 => гипотенуза = стороне = 13 ×2=26