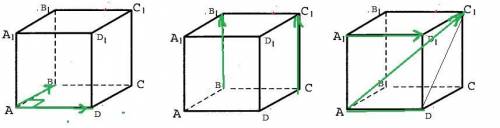
В кубе ABCDA1B1C1D1 найдите угол между векторами:
a)AB и AD , б)BB1 и CC1 , в)AC1 и A1D1
Объяснение:
Углы между векторами а)∠АВ,АD=90°, т.к все грани куба являются квадратами.
б) ∠ВВ₁,СС₁=0°, т.к эти вектора лежат на параллельных прямых.
в) ∠АС₁,А₁D₁=arcctg√2.
Т.к. вектор А₁D₁=AD , то найдем угол ∠АС₁,АD
Из ΔВСС₁ -прямоугольный. Пусть ребро куба а, тогда по т. Пифагора
ВС₁=а√2.
По т. о трех перпендикулярах если проекция ВС перпендикулярна , прямой лежащей в плоскости АВ, то и наклонная С₁В перпендикулярна прямой лежащей в плоскости АВ⇒ ΔАВС₁-прямоугольный .
tg∠С₁FD=BС₁/AB или tg∠С₁FD=а√2/а , tg∠С₁FD=√2 , ∠С₁FD=arctg√2,
а значит у угол между векторами ∠АС₁,А₁D₁=arcctg√2.
14) Найдите | 2а-в| , если | а|=3, | в|=4, а*в=4.
15) Длины векторов а и в равны 3 и 4 соответственно . Чему может равняться | 2а-в| : 0; 6 ; 1; 11 ?
22) Укажите уравнение прямой , чтобы точки А(а;-1) ,В(1-а ;2а+1) ,С(а+1;-3) лежали на одной прямой?
Объяснение:
14)
а*в=| а|*| в|*cos(∠а,в), значит 4=3*4*cos(∠а,в), или cos(∠а,в)=1/3
Тогда длину | 2а-в| можно найти по т. косинусов , т.к ∠(а,в)=∠(2а,в) , см. на чертеже.
| 2а-в| = | КР| , | 2а| = | ОК| , | в| = | ОР|
КР²=ОК²+ОР²-2*ОК*ОР*cos∠(2а,в) ,
КР²=6²+4²-2*6*4*1/3 ,
КР²=52-16 , КР²=36 , ⇒КР=6 ,| 2а-в| =6 .
15) доделаю
16) Условие при котором три точки А(х₁;у₁) , В(х₂;у₂) , С(х₃;у₃) лежат на одной прямой :(у₃-у₁):(у₂-у₁)=(х₃-х₁):(х₂-х₁).
Подставляем координаты А(а;-1) ,В(1-а ;2а+1) ,С(а+1;-3) :
(-3+1):(2а+1+1)=(а+1-а):(1-а-а) или -2:(2а+2)=1:(1-2а) или 2а+2=-2+4а или а=2. Тогда А(2;-1) ,В(-1 ;5)
Уравнение( каноническое) прямой проходящей через А(х₁;у₁) , В(х₂;у₂) : (х-х₁):(х₂-х₁)=(у-у₁):(у₂-у₁).
Подставим (х-2):(-1-2)=(у+1):(5+1) , получим 2(х-2)=-1(у+1) или
у=3-2х или у=-2х+3
ответ: Странное у тебя условие: выбрать ВЕРНЫЕ утверждения, но записать в ответ НЕВЕРНЫЕ.
ВЕРНЫЕ утверждения: 1359
НЕВЕРНЫЕ утверждения: 2467810
Объяснение:
Первое утверждение верное, так как логарифм определен на промежутке(0;+Беск), других ограничений нет на функцию, значит она определена именно на этом промежутке
Второе утверждение неверное исходя из первого
Третье утверждение верное, так как точка 0,5 является точкой максимума функции. Найдя производную и приравняв к нулю, получим (0)+[0,5]- что и доказывает данное утверждение
Четвертое утверждение неверное исходя из третьего
Пятое утверждение верное исходя из третьего
Шестое утверждение неверное исходя из третьего и пятого
Седьмое утверждение неверное т.к. при поиске производной мы найдем значение х =0,5 что является экстремумом функции
Восьмое утверждение неверное из седьмого
Девятое утверждение верное(доказал в третьем утверждении)
Десятое утверждение неверное так как точка 1 не является точкой экстремума