Высота в равностороннем треугольнике является также медианой и биссектрисой, значит АД=ДС, угол АВД= углу ДВС. Равенства треугольников АВД и ВДС можно доказать по всем трем признакам равенства треугольников: 1)по двум сторонам и углу между ними: АВ=ВС из дано, сторона ВД общая и угол АВД равен углу ДВС 2)по стороне и двум прилежащим углам:сторона ДВ общая, углы АВД и ДВС равны, углы АДВ и ВДС равны и прямые, так как ВД - высота. 3) по трем сторонам: АВ=ВС из дано, сторона ВД одщая, и АД равно ДС, так как ВД это и медиана тоже.
5. 28
6. 21
Объяснение:
5. АВ = 42, 2BC = AC - это если наше условие написать на математическом языке. Чтобы решить эту задачу, нужно составить уравнение
AC + BC = 42
Но чтобы у нас не было двух неизвестных, нужно один отрезок выразить через другой. Для этого мы и переписали условие
АС + BC = 2BC + BC
2BC + BC = 42
3BC = 42
BC = 42 : 3 = 14
Если BC = 14, то АС = 42 - 14 = 28.
6. АВ = 49, АС =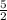 CB или 2,5СВ
CB или 2,5СВ
Чтобы найти АС, мы переписали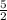 в 2,5 , чтобы проще было посчитать. АС - это две части и одна половинка этой части СВ. То есть,
в 2,5 , чтобы проще было посчитать. АС - это две части и одна половинка этой части СВ. То есть,
СВ + СВ +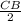 = AC.
= AC.
СВ + СВ +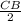 + СВ = 49
+ СВ = 49
3СВ +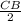 = 49, чтобы легко избавиться от некрасивой дроби, нужно две части уравнения домножить на 2
= 49, чтобы легко избавиться от некрасивой дроби, нужно две части уравнения домножить на 2
6СВ + СВ = 98
7СВ = 98
СВ = 14, следовательно АС = 49 - 14 = 35
Раз нам надо найти АС - СВ, то 35 - 14 = 21.