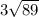
Объяснение:
Объём пирамиды:
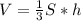, где S - площадь основания, h - высота пирамиды.
Значит 
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна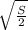 
Тогда, по теореме Пифагора:
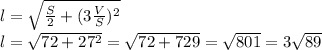
При пересечении двух прямых образовались 4 угла,и эти четыре угла равны 360 градусов,получилось две пары вертикальных углов
<АОD=<COB,как вертикальные
<АОС=<DOB,как вертикальные
<АОD=X
<COB=X
<AOC=2X
<DOB=2X
X+X+2X+2X=360 градусов
6Х=360
Х=360:6
Х=60
<АОD=<COB=60 градусов
<АОС=<DOB=60•2=120 градусов
Объяснение:
Вопрос стоит так-сумма двух углов равна градусной мере третьего угла
Два вертикальных угла по 60 градусов,а один угол из другой пары вертикальных углов равен 120 градусов
60+60=120 градусов,что и следовало доказать