1)
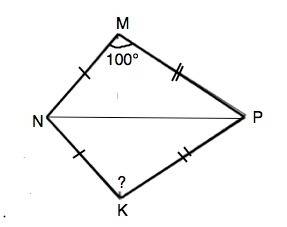
Проведем диагональ NP. Треугольники PMN и PKN равны по трем сторонам - две по условию, третья - общая. .
Следовательно, углы при вершинах К и М равны. Угол К=100°
2)
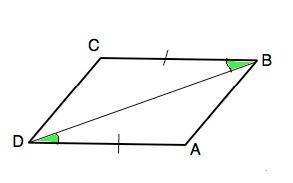
Диагональ BD делит четырехугольник на треугольники ∆ ABD и ∆ CBD. В этих треугольниках стороны ВС=АD по условию, DB общая, углы между этими сторонами равны. ∆ ABD и ∆ CBD равны по первому признаку равенства треугольников.
Следовательно, стороны АВ=CD.
Если противоположные стороны четырехугольника равны, этот четырехугольник - параллелограмм. ⇒, АВ||CD. Доказано.
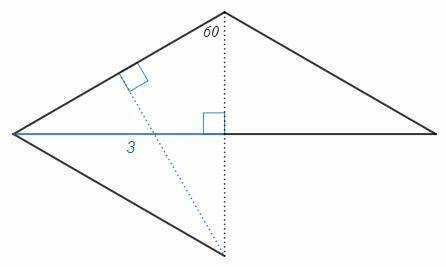
В равнобедренном треугольнике углы при основании равны, в треугольнике не может быть двух тупых углов, следовательно только угол против основания может равен 120.
Серединный перпендикуляр к основанию равнобедренного треугольника является также биссектрисой - делит угол против основания на два угла по 60, и медианой - делит основание на два отрезка по 3.
Точка пересечения серединных перпендикуляров является вершиной равнобедренного треугольника с основанием на боковой стороне (любая точка серединного перпендикуляра равноудалена от концов отрезка). Равнобедренный треугольник с углом 60 - равносторонний. В равностороннем треугольнике высоты равны.
Расстояние от точки пересечения серединных перпендикуляров до боковой стороны равно 3.