
Объяснение:
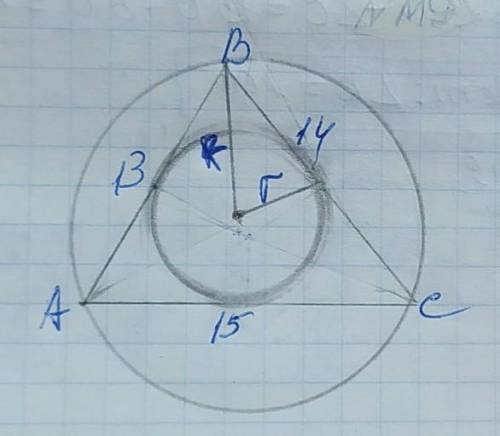
6) Обозначим вершины треугольника АВС. R радиус описанной окружности найдём по формуле:
R=(abс)/(4S) где abc – стороны треугольников, а S –его площадь.
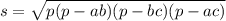
где р – полупериметр.
р=(АВ+ВС+АС)/2=(13+14+15)/2=42/2=21
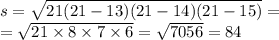
S=84(ед²)
R=(13×14×15)/(4×84)=2730/336=8,125(ед)
r=S/p – где r –радиус вписанной окружности, а р – полупериметр.
r=84/21=4(ед)
ОТВЕТ: r=4(ед); R=8,125(ед)
7) а(2; –6); b(–6; 2); c(2a+b)–?
2a=(2×2; –6×2)=(4; –12)
2a+b=(4+(–6); –12+2)=(–2; –10)
2a+b(–2; –10)
Абсолютная величина вектора 2а+b:
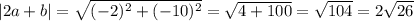
ОТВЕТ: координаты вектора 2а+b(–2; –10);
абсолютная величина вектора 2а+b=2√26
Будем считать, что у отрезков есть начальная и конечная точки, то есть направление. Теперь у нас направленные отрезки (векторы).
Если точки расположены последовательно A_C, то имеем вектор AC.
Если точки расположены последовательно C_A, то имеем вектор -AC.
AM =1/2 AB =1/2 (AC+CB)
CK =1/2 CD =1/2 (CB+BD)
AK =AC+CK =AM+MK
AC +1/2 CB +1/2 BD = 1/2 AC +1/2 CB +MK => MK =1/2 AC +1/2 BD
1) Точки расположены последовательно A_C, B_D
MK =1/2 (AC+BD) = |5+7|/2 =6
2) Точки расположены последовательно C_A, B_D
MK =1/2 (-AC+BD) = |-5+7|/2 =1
3) Точки расположены последовательно A_C, D_B
MK =1/2 (AC-BD) = |5-7|/2 =1
4) Точки расположены последовательно C_A, D_B
MK =1/2 (-AC-BD) = |-5-7|/2 =6