
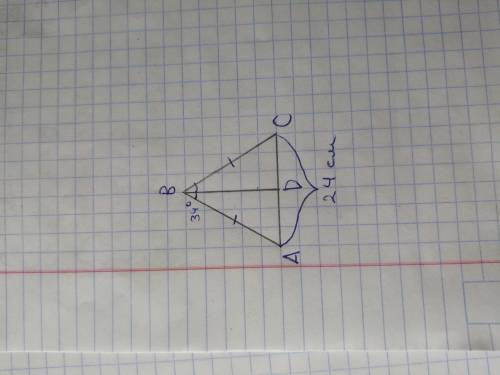
Дано: треугольник ABC - равнобедренный;
BD - биссектриса;
угол ABD = 34°;
AC = 24 см
Найти: угол B; угол BDC; сторону DC
1) ∠В = 2 × ∠ABD = 2 × 34° = 68°, т. к. BD - биссектриса делит Abc на равные углы.
2) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является высотой => BD⊥AC и ∠BDC = 90°.
3) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является медианой => DC = 1/2 × AC = 1/2 × 25 = 12,5 см.
ответ: ∠В = 68°; ∠BDC = 90°; DC = 12,5 см.
значит H=2
2)Радиус основания равен половине стороны треугольника=10/2=5
высота равностореннего треугольника имеет формулу:(а*корень из 3)/2
подставляем:(10*корень из 3)/2=5*корень из 3
3) осевое сечение цилиндра-прямоугольник
если диагональ прямоугольника =20 и угол 60,то нижняя сторона прямоугольника =10(лежит на против угла в 30 градусов),вторая сторона прямоугольника равна по теореме Пифагора корень из 300=10*корень из 3
10-это диаметр цилиндра,радиус тогда=5
10*корень из 3-высота цилиндра
подставляем в формулу боковой поверхности:2*п*5*3*корень из 3=30П*корень из 3