Задача

Дана окружность с центром О.

Длина перпендикуляра ON, подведенного к хорде DC данной окружности, равна 12 см.

Вычислите радиус данной окружности,

если сумма углов ODN и NCO равна 60 градусов.

Сначала нужно начертить все имеющиеся окружности и углы.
Потом написать дано и краткое решение.И ответ.

👇

Открыть все ответы

Ответ:

ILoveChemistry2

29.01.2022

Случай 1 : Площадь бо́льшего треугольника равна 8 (ед²).Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.

Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).

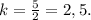
$k = \frac{5}{2} = 2,5.$

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Отсюда -

$\frac{S_{1} }{S_{2} } = k^{2} \\\\\frac{8}{S_{2} } = 2,5^{2} \\\\\frac{8}{S_{2} } = 6,25\\\\S_{2} = \frac{8}{6,25} \\\\\boxed{S_{2} = 1,28}$

1,28 (ед²).

- - -

Случай 2 - Площадь меньшего треугольника равна 8 (ед²).

В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).

S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника

Тогда -

$k = \frac{2}{5} = 0,4.$

$\frac{S_{2} }{S_{1} } = k^{2}\\\\\frac{8 }{S_{1} } = 0,4^{2}\\\\\frac{8 }{S_{1} } = 0,16\\\\S_{1} = \frac{8}{0,16}\\\\\boxed{S_{1} = 50}$

50 (ед²).

4,5(61 оценок)

Ответ:

HelpMePzhalsta

29.01.2022

В треугольнике: катеты а и b, гипотенуза с, прямой угол С,
R - радиус описанной окружности, r- радиус вписанной окружности.
Начнём с описанной окружности. Поскольку угол С прямой, то этот угол опирается на диаметр окружности, т.е. диаметр окружности есть его гипотенуза, и. с = 2R
Теперь вписанная окружность. Опустим из её центра на катеты перпендикуляры, эти перпендикуляры равны r- радиусу вписанной окружности. Два взаимно перпендикулярных радиуса r и отрезки катетов, прилежащих к вершине прямого угла С, образуют квадрат со стороной r.
Тогда отрезки катетов, прилегающих к вершинам острых углов, равны
(а - r) и (b - r).
Третий перпендикуляр, опущенный из центра окружности на гипотенузу делит её на отрезки, равные (а - r) и (b - r).
Получается, что гипотенуза равна c = a - r + b - r = a + b - 2r.
Но ранее мы получили, что с = 2R
Тогда 2R = a + b - 2r
2R + 2r = a + b
R + r = 0.5(a + b) что и требовалось доказать.

4,6(85 оценок)

Это интересно:

17.04.2022

Как избежать наказания в школе: 10 простых советов...

Праздники-и-традиции

24.12.2020

Как правильно чистить искуственную елку...

Компьютеры-и-электроника

03.01.2023

Как активировать iMessage на вашем устройстве: шаг за шагом...

Кулинария-и-гостеприимство

14.12.2022