Стороны относятся как 1 к 4, а их двойная сумма равна 30
2(x+4x)=30
5x=15
x=3
Значит, одна сторона равна 3 см, а вторая 12 см.
Проведём высоты в параллелограмме.
Т.к по условию острый угол равен 30 градусов, то синус его градусной меры равен отношению высоты к гиппотинузе( в данном случае меньшей стороне параллелограмма).
Пусть основания ВС и AD. Обозначим точку пересечения диагоналей - точку О. Проведем высоту через точку пересечения диагоналей. Высота делит основания равнобедренной трапеции пополам. Пусть отрезок высоты в треугольнике ВОС равен х, а отрезок высоты в треугольнике AOD равен (h-x). BC/2=x·tg((180°-α)/2) AD/2=(h-x)· tg((180°-α)/2)
1. Задача 1. решена пользователем ХироХамаки Новичок (решение в файле)
2. Условие задачи 2. неточное. Должно быть: Основание АС равнобедренного треугольника лежит в плоскости α. Найдите расстояние от точки В до плоскости α, если АВ = 5, АС = 6, а двугранный угол между плоскостью треугольника и плоскостью α равен 60 градусам.
Проведем ВН⊥АС и ВО⊥α. ВО - искомое расстояние. ОН - проекция ВН на плоскость α, значит ОН⊥АС по теореме, обратной теореме о трех перпендикулярах. ∠ВНО = 60° - линейный угол двугранного угла между плоскостью α и плоскостью треугольника. АН = НС = 6/2 = 3 (ВН - высота и медиана равнобедренного треугольника) ΔАВН: по теореме Пифагора ВН = √(АВ² - АН²) = √(25 - 9) = √16 = 4 ΔВНО: ВО = ВН · sin 60° = 4 · √3/2 = 2√3
3. АО⊥α, ОВ и ОС - проекции наклонных АВ и АС на плоскость α, тогда ∠АВО = ∠АСО = 60°. ΔАВО = ΔАСО по катету и противолежащему острому углу (АО - общий катет и ∠АВО = ∠АСО = 60°), значит АВ = АС = 6.
Стороны относятся как 1 к 4, а их двойная сумма равна 30
2(x+4x)=30
5x=15
x=3
Значит, одна сторона равна 3 см, а вторая 12 см.
Проведём высоты в параллелограмме.
Т.к по условию острый угол равен 30 градусов, то синус его градусной меры равен отношению высоты к гиппотинузе( в данном случае меньшей стороне параллелограмма).
Значит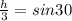
h=3*sin30
h=1.5 см.
S=12*h=18 см^2
ответ: 18 см^2