ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
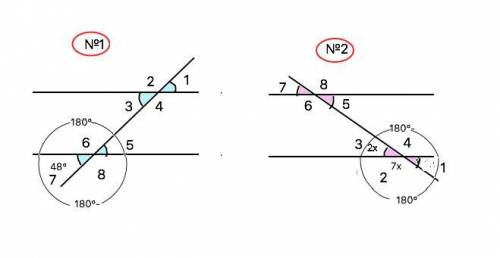
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
Дано:тр. ABC, BD=DA, BF=FC, DF
Доказать: DF||AC, DF=1/2 AC
Допустим, что DF не параллельна AC . Тогда из середины D стороны AB проведем прямую, параллельную AC, которая пересечет сторону BC не в точке F. Но эта точка по теореме будет также серединой стороны BC. Получилось, что у BC две середины, что невозможно, а поэтому допущение неверно. Следовательно, DF||AC, т.е. средняя линия параллельна третьей стороне.
Возьмем AE=AC, тогда DE - средняя линия и DE||BC (по доказанному) . DFCE — параллелограмм, поэтому DE=EC=1/2 AC(так как AE=EC по построению).