Если вас еще интересует решение этой задачи, то здесь не так уж и сложно.
Нужно воспользоваться формулами для нахождения диагоналей параллелограмма через его стороны.
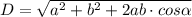
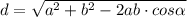
D - большая диагональ, d - малая диагональ.
Подставляем длины сторон и диагоналей и находим угол 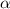
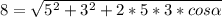
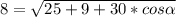
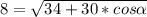
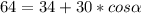
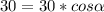
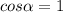

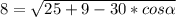

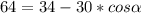
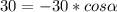
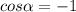
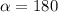
Как видим, углов между сторонами 5 и 3, при которых одна из диагоналей могла бы равняться 8, и при которых сещуствовал бы параллелограмм, нет.
Вот и вывод: диагональ параллелограмма не может равняться 8 при сторонах 5 и 3.
(х2 - это х в квадрате). решив его , найдешь длину х, ширина, соответственно, на 2 см меньше. Если увеличены на 4 см обе стороны, то уравнение: (х+4)*(х-2+4) = 48, (х+4)*(х+2) = 48; х2+4х+2х+8 = 48;
х2+6х-40 = 0, в этом случае, D = 9 +40=49 (т.к. уравнение приведенное, а b -четное), х = 10см - это длина, ширина - 8см