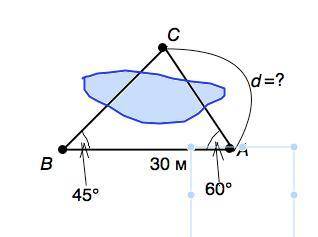
Объяснение: Чтобы найти расстояние d от пункта A до недоступного пункта C, на местности выбрали точку B и измерили длину с отрезка AB и углы α и β. Найдите расстояние от пункта A до пункта C, если AB = 30 м, α = 60°, β = 45°
————
Сделав рисунок по условию задачи, получим треугольник АВС с основанием АВ и углами ∠САВ=60° и ∠СВА=45°.
Из суммы углов треугольника ∠АСВ=180°-(45°+60°)=75°
По т.синусов АВ:sin75°=AC:sin45°.
Табличное значение sin75°= (√3+1)/2√2; sin45°=√/2 ⇒
30•2√2:(√3+1)=d:(√2/2) ⇒
AС=d= 60/(√3+1) или ≈ 21,96 м.
4.Это параллелограммы,т.к. АB||KL,АК||BL и KL||CD ,KD||LC.Противоположные стороны попарно параллельны,это признак параллелограмма.
3.Пусть один из углов=х,тогда другой будет 3х. х+3х=180.4х=180 х=45,3х=135.ответ:45,45,135,135
4.В данном четырехугольнике диагонали равны диаметру,значит,равны между собой.Точкой пересечения делятся пополам.Это признак прямоугольника.
3.Пусть одна из сторон х.Периметр=2х+2*8=36 2х=20 х=10
ответ:8,10,10
4.В данном четырехугольнике диагонали равны диаметру и равны между собой,пересекаются под прямым углом и точкой пересечения делятся пополам.Это признак квадрата.