В ромбе диагонали точкой пересечения делятся пополам (АО=ОС и ВО=OD).
Пусть ВО=х, тогда:
AC-BD=14
AC-2x=14
AC=14+2x
2·OC=2(x+7)
OC=x+7
Из ΔBCO по т. Пифагора:
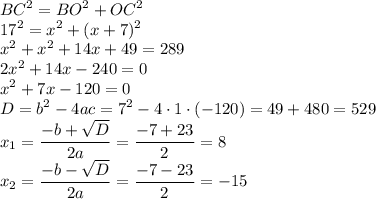
x=-15 не подходит по смыслу задачи, поэтому один корень х=8.
ВО=х=8 см
ОС=х+7=8+7=15 см
АС=АО+ОС=15+15=30 см
BD=BO+OD=8+8=16 см
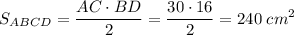
Вспомним такую формулу: 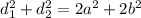 , где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
, где d₁, d₂ - диагонали параллелограмма(у нас ромб, а ромб-это тоже параллелограмм), a, b - стороны параллелограмма(у нас ромб, поэтому a=b).
Найдем диагонали, составив систему:
Пусть АС=х, BD=y.
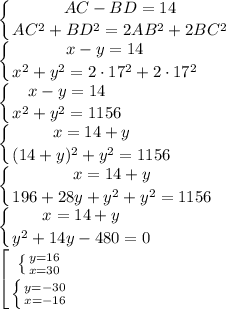
Отрицательные значения нам не подходят, так как длинна - величина неотрицательная.
Тогда AC=x=30см, BD=y=16см.
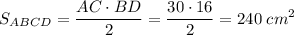
ответ: 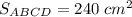
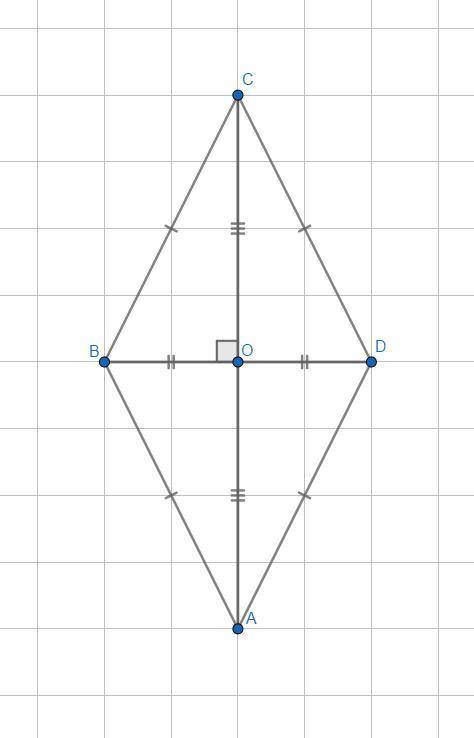
Объяснение:
d₁-d₂=14
d₁=14+d₂
Діагоналі у точці перетину діляться навпіл і утворюють прямокутні трикутники.Катети дорівнюють половинам діагоналей: 14+d₂ / 2 та d₂/2.
За теоремою Піфагора:
17²=(14+d₂ /2)²+ (d₂/2)²
289=(14+d₂)² /4+d₂²/4
289*4=(14+d₂)² +d₂²
1156=14²+28d₂+d₂²+d₂²
2d₂²+28d₂-960=0 :2
d₂²+14d₂-480=0
D = b² - 4ac = 14² - 4·1·(-480) = 196 + 1920 = 2116
x₁ = -14 - √2116 /2·1 = -14 - 46/ 2 = -60 /2 = -30 не підходить
x₂ = -14 + √2116/ 2·1 = -14 + 46 /2 = 32/ 2 = 16 см -d₂
d₁=16+14 = 30 см
S=1/2× 16×30=240 см²
Пусть даны две прямые
y=k _{1} xy=k
1
x ,y=k _{2} xy=k
2
x
Причем tg \alpha _{1}=k _{1}tgα
1
=k
1
tg \alpha _{2} =k _{2}tgα
2
=k
2
Найдем тангенс угла между этими прямыми:
tg( \alpha _{1} - \alpha _{2})= \frac{tg \alpha _{1}-tg \alpha _{2} }{1+tg \alpha _{1}tg \alpha _{2} }= \frac{k _{1}-k _{2} }{1+k _{1}k _{2} }tg(α
1
−α
2
)=
1+tgα
1
tgα
2
tgα
1
−tgα
2
=
1+k
1
k
2
k
1
−k
2
Прямые перпендикулярны, угол между ними 90⁰. Тангенс 90⁰ не существует, значит в последней дроби знаменатель равен 0,k _{1} k _{2} =-1k
1
k
2
=−1
это необходимое и достаточное условие перпендикулярности двух прямых
y=k _{1}xy=k
1
x ,y=k _{2} xy=k
2
x
Данная прямая может быть записана в виде y= \frac{5}{2} x+ \frac{7}{2}y=
2
5
x+
2
7
Угловой коэффициент равен 5/2,
Значит угловой коэффициент перпендикулярной ей прямой будет равен (-2/5).
ответ. y=- \frac{2}{5}xy=−
5
2
x
И все прямые ей параллельные, то есть
y=- \frac{2}{5}xy=−
5
2
x +С,
где С- любое действительное число
Объяснение:
решение не мое