1. Изображение и обозначение точек, прямых, отрезков. Понятие длины отрезка. Единицы измерения отрезков. Приборы для измерения длин.
2. Основное свойство прямой. Определение пересекающихся прямых. Теорема о пересекающихся прямых.
3. Изображение и обозначение лучей, углов. Понятие дополнительных лучей. Вершина и сторона угла.
4. Определение равных углов. Понятие биссектрисы угла. Единицы измерения углов. Приборы для измерения углов.
5. Понятие и обозначение середины отрезка. Определение равных отрезков. Основное свойство отрезка.
6. Понятие прямого, тупого, острого и развернутого углов. Градусные меры углов. Основное свойство величины угла.
7. Понятие и изображение смежного и вертикального углов. Свойства смежных и вертикальных углов. *Доказательство одного из свойств.
8. Понятие и обозначение перпендикулярных прямых. Теорема о единственной прямой, перпендикулярной данной. *Доказательство теоремы.
9. Понятие и изображение вершин и сторон треугольника. Понятие периметра треугольника. Определение равных треугольников. Обозначение попарно равных элементов равных треугольников.
10. Понятие серединного перпендикуляра. Теорема о серединном перпендикуляре. *Доказательство теоремы.
11. Теорема «Первый признак равенства треугольников». Обозначение первого признака равенства на чертеже. *Доказательство теоремы.
12. Теорема «Второй признак равенства треугольников». Обозначение второго признака равенства на чертеже. *Доказательство теоремы.
13. Медианы, биссектрисы и высоты треугольника. Изображение медиан, биссектрис и высот на чертеже. Точка пересечения высот остроугольного, прямоугольного и тупоугольного треугольников.
14. Понятие и изображение равнобедренного треугольника. Вершина, основание и боковые стороны равнобедренного треугольника. Понятие равностороннего треугольника и его обозначение на чертеже.
15. Свойства равнобедренного треугольника. *Доказательство одного из свойств.
16. Признаки равнобедренного треугольника. *Доказательство одного из признаков.
17. Теорема «Третий признак равенства треугольников». Обозначение третьего признака равенства на чертеже. *Доказательство теоремы.
18. Определение, изображение и обозначение параллельных прямых.
19. Признаки параллельности двух прямых (три теоремы). Понятие, изображение и обозначение накрест лежащих, односторонних и соответственных углов. *Доказательство одной из теорем
20. Теоремы об углах, образованных двумя параллельными прямыми и секущей (три теоремы). *Доказательство одной из теорем
21. Теорема о сумме углов треугольника. Понятие и изображение внешних углов треугольника. Понятие и изображение остроугольного, тупоугольного и прямоугольного треугольников.
22. Прямоугольный треугольник. Изображение и определение катетов и гипотенузы прямоугольного треугольника. Свойства прямоугольного треугольника (сумма острых углов; катет, лежащий против угла в 30°).
23. * Признаки равенства прямоугольных треугольников (четыре теоремы). Изображение признаков на чертеже.
24. Понятие расстояния между точками, расстояние от точки до прямой. Понятие и изображение перпендикуляра и наклонной. Расстояние между параллельными прямыми.
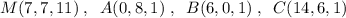
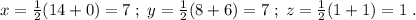
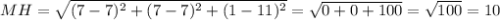
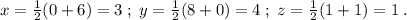
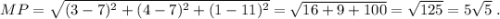
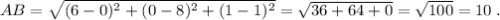
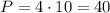 .
.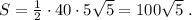
ВО = ДО = 5 см
АМ = СМ = √(9²+12²) =√(81+144) = √225 = 15 см
МС = МД = √(5²+12²) =√(25+144) = √169 = 13 см
Расстояния между основаниями? Это как? Стороны и диагонали ромба?
AB = BC = СД = АД = √(9²+5²) =√(81+25) = √106 см
АС и ВД даны по условию.
---
2 варианта, к сожалению!
1) АС - гипотенуза
AO = AC/2 = 7,5 см
О - центр описанной окружности треугольника АВС и поэтому
АК = ВК = СК = √(7,5² + 8,5²) = √(15² + 17²)/2 = √(225+289)/2 = √514/2 см
2) AB - гипотенуза
АВ = √(8² + 15²) = √(64+225) = √289 = 17 см
AO = AВ/2 = 8,5 см
АК = ВК = СК = √(8,5² + 8,5²) = 8,5√2 см