
Дано:
SABC - пирамида
SО - высота
AB=8см
ã=45°
V-?
Объем пирамиды: V=1/3×Sосн×h
В основании лежит правильный треугольник, площадь которого S=a²√3/4=8²√3/4=16√3см².
Высота правильного треугольника: h=a√3/2= 8√3/2=4√3см.
Точка, на которую опущена высота, является серединой правильного треугольника (точка пересечения медиан). Эти медианы делятся в отношении 2:1 от вершины.
AO=2×4√3/3=8√3/3.
Рассмотрим треугольник AOS, у которого O=90°, A=S=45°. Если два угла равны 45°, то их катеты равны. Значит, высота пирамиды равна 8√3/3.
Найдем объем:
V=1/3×16√3×8√3/3=128/3 см³
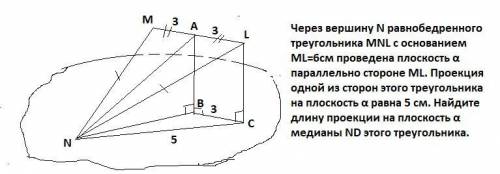
Через вершину N равнобедренного Δ MNL с основанием ML=6см проведена плоскость α параллельно стороне ML. Проекция одной из сторон этого треугольника на плоскость α равна 5 см. Найдите длину проекции на плоскость α медианы ND этого треугольника.
Объяснение:
Проекцией, равной 5 см , не может быть сторона ML=6 , т.к. ML║α .
Пусть LC, АВ -перпендикуляры к плоскости α. Тогда LC=AB. тк ML║α .
Проекцией стороны NL на плоскость α будет отрезок NC=5 см( отрезок между основанием перпендикуляра и основанием наклонной) , а проекцией медианы NA будет отрезок NB.
МА=АL=3 см . АВСL-прямоугольник , поэтому ВС=3 см,
Т.к медиана NB равнобедренного ΔNCO, является высотой , то ΔNBC- прямоугольный , по т. Пифагора NB=√(5²-3²)=4 (см).
600 : 1,8 = 6000 :18 = 333. 33333