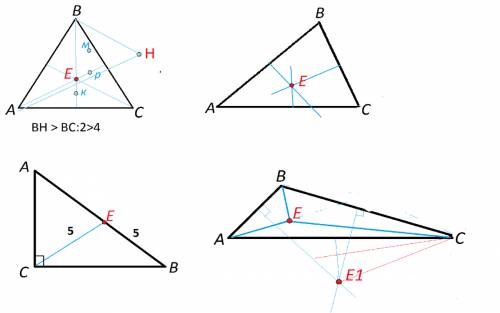
Объяснение:
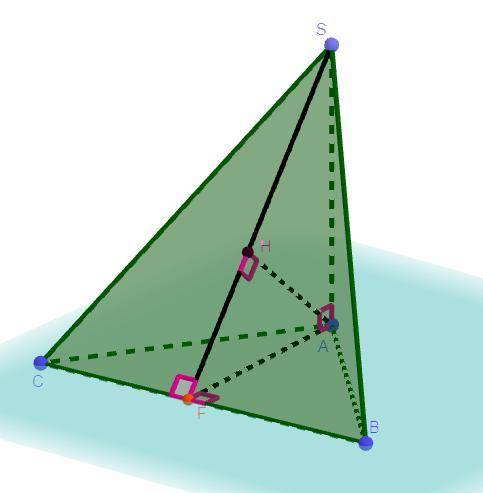
Дано: Пирамида ABCS, AS ⊥ ABC, AB = AC = BC = 4, AS = 12, AH ⊥ SBC
Найти: AH - ?
Решение: Проведем высоту в треугольнике ΔABC к стороне BC в точку F, так как по условию треугольник ΔABC - равносторонний, то по свойствам равностороннего треугольника его высота является биссектрисой и медианой, следовательно BF = CF. Треугольник ΔCAS = ΔBAS(AS ⊥ ABC по условию, поэтому треугольник ΔCAS и ΔBAS - прямоугольные) по двум катетам, так как AS - общая и AC = BC по условию, из равенства треугольников следует, что SC = SB, тогда треугольник ΔSCB - равнобедренный. Проведем отрезок SF, так как треугольник ΔSCB - равнобедренный(SC = SB, следовательно BC - основание), то по теореме медиана опущенная на высоту является биссектрисой и высотой, тогда SF ⊥ BC.
Так как по условию AH ⊥ SBC, то AH перпендикулярно любой прямой лежащей в плоскости SBC, то AH ⊥ SF (SF ∈ SBC), так как SF - гипотенуза прямоугольного треугольника ΔSAF (по условию AS ⊥ ABC) и так как SF - гипотенуза прямоугольного треугольника ΔSAF (по условию AS ⊥ ABC), то отрезок AH - высота прямоугольного треугольника ΔSAF проведенная к гипотенузе.
Рассмотрим прямоугольный треугольник ΔCAF(AF ⊥ BC по построению). Так как треугольник ΔABC - правильный по условию, то по свойствам правильного треугольника все его углы 60°, следовательно ∠BCA = 60°. 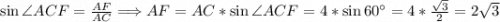 .
.
Рассмотрим треугольник ΔSAF, по теореме Пифагора: 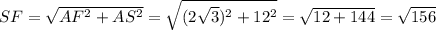 .
.
По формуле площади прямоугольного треугольника: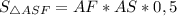 , с другой стороны
, с другой стороны 
AS * AF * 0,5 = AH * SF * 0,5|:0,5SF
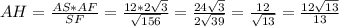 .
.
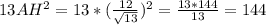 .
.
РАССМОТРИМ ТРЕУГОЛЬНИК ВДЕ И CДF-ПРЯМОУГОЛЬНЫЕ(Т.К. ДЕ, ДF- ПЕРПЕНДИКУЛЯРЫ)
ВДЕ=СДF-ПО УСЛОВИЮ
BD=CD- ПО УСЛОВИЮ
ЗНАЧИТ,ВДЕ=CDF(ПО ГИПОТЕНУЗЕ И ОСТРОМУ УГЛУ) И УГОЛ ЕВД=ДСF, ЗНАЧИТ,АВС РАВНОБЕДРЕННЫЙ