
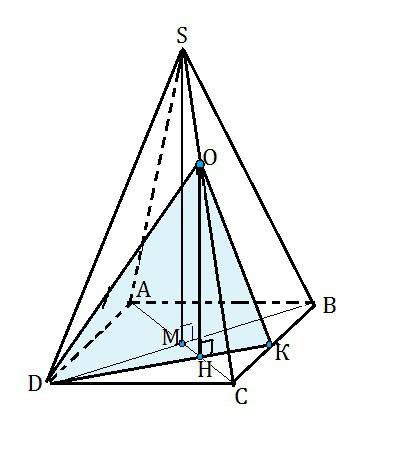
SABCD -правильная четырехугольная пирамида. Постройте сечение пирамиды плоскостью, проходящей через DO (точка О-внутренняя точка отрезка SC) и перпендикулярной плоскости ABC.
Если искомая площадь перпендикулярна плоскости АВС, то она перпендикулярна плоскости АВСD.
Проведем диагональное сечение АSС пирамиды .
О лежит на ребре SC и принадлежит этому диагональному сечению.
Опустим в плоскости ∆ ASC из О перпендикуляр ОН на АС (он лежит в плоскости диагонального сечения, перпендикулярной основанию, параллелен высоте пирамиды, и потому перпендикулярен её основанию).
Через D и Н проведем прямую до пересечения с ВС в точке К.
Соединим D, О и К.
Через 3 точки можно провести плоскость, притом только одну.
Плоскость ∆ DОК - сечение пирамиды.
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Плоскость ∆ DОК проходит через ОН, перпендикулярный плоскости основания, и является искомым сечением
Прямая, проходящая через точку А0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Уравнение прямой :
y = -7/2x + 56 или 2y +7x -112 = 0
Данное уравнение можно найти и другим Для этого найдем угловой коэффициент k1 прямой .
Уравнение AB: , т.е. k1 = 2/7
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим :
2/7k = -1, откуда k = -7/2
Так как искомое уравнение проходит через точку A и имеет k = -7/2,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = 20, k = -7/2, y0 = -14 получим:
y-(-14) = -7/2(x-20)
или
y = -7/2x + 56 или 2y + 7x - 112 = 0