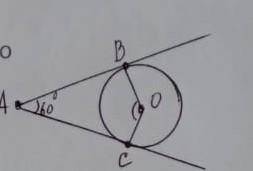
Примем отрезки, на которые делится гипотенуза точкой касания, равными x и y.
Тогда один катет равен 1 + x, второй равен 1 + y (с учётом свойства касательных из одной точки к окружности).
Составим систему.
Первое уравнение: по Пифагору: (1 + x)² + (1 + y)² = 5²,
второе: x + y = 5.
Сделаем замену: у = 5 - х и подставим в первое уравнение.
(1 + x)² + (1 + (5 - х))² = 5².
1 + 2x + x² + 36 - 12x + x² = 25.
2x² - 10x + 12 = 0 или, сократив на 2:
x² - 5x + 6 = 0. Д = 25 - 4*1*6 = 1. х1 = (5 + 1)/2 = 3, х2 = (5 - 1)/2 = 2.
ответ: отрезки равны 3 и 2.
ответ: ниже
Объяснение: На фото рисунок и используемые теоремы (синусов и косинусов)
Чтобы найти сторону ВС, воспользуемся второй
cos110º= -0,342
BC=√(АС²+ВA²-2*AC*BA*cosA)=
=√(10²+6²+2*10*6*0,342)=
=√(100+36+41,04)=√(100+36+41,04)=13,3 (округлено)
sin110º=0,94
По теореме синусов находим синус одного из неизвестных углов
AC/sinB=BC/sin110º
sinB=AC*sin110º/BC=
=10*0,94/13,3= 0,707 округлено => <В=45º приблизительно
Зная, что сумма всех углов треугольника равна 180º, сожем найти и третий угол
<С=180º-110º-45º=25º