Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
ВО:ОК=2:1
SO:ON=2:1
В равностороннем треугольнике медианы равны. Следовательно, равны и их сходственные отрезки.
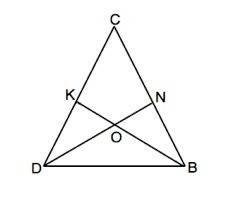
В ∆ DOK и ∆ BON равны две стороны и углы между ними при вершине О как вертикальные. Следовательно, эти треугольники равны по первому признаку.
--------
∆ DOK и ∆ BON равны и по 3-му признаку, т.к. у равных сторон равны и их половины.
А, поскольку медианы являются здесь и биссектрисами и высотами, то можно доказать их равенство и по второму признаку.
Угол между плоскостями - это линейный угол, образованный сечением этих плоскостей плоскостью, перпендикулярной к их линии пересечения.
В нашем случае это угол DHD1, где DH и HD1 - перпендикуляры к АВ. В прямоугольном треугольнике DHD1 с прямым углом D1 катет HD1 равен HD1=HD*Cosβ. Cosβ=√(1-sin²β)=√(1-1/16)=√15/4. Тогда HD1=((9*√5)/4)*(√15/4)=45√3/16. Площадь параллелограмма равна S=a*h, где а - сторона параллелограмма, а h - высота, опущенная на эту сторону. В нашем случае а=9, h=45√3/16.
S=9*45√3/16=405√3/16