Назовем точки пересечения вписанной в трапецию окружности со сторонами ВС и АД соответственно К и М. Тогда КМ является высотой трапеции и равна 2-м радиусам окружности, т.е. 6см. Площадь трапеции = (ВС+АД)/2*КМ=60. Т.е. ВС+АД=20. По теореме вписанной в 4-угольник окружности: ВС+АД=АВ+СД. Но т.к. АВ=СД, то АВ=СД=20/2=10. В трапеции углы С и Д односторонние, т.е. С+Д=180. Центр вписанной окружности лежит на пересечении биссектрис. Значит угол ОСД=ВСД/2 и СДО=СДА/2. Тогда ОСД+СДО=180/2=90. Рассмотрим треугольник ОСД: угол СОД=180-(ОСД+СДО)=90. Перейдем к описанной возле треугольника ОСД окружности. Т.к. треугольник прямоугольный, то центр окр-ти лежит на середине гипотенузы. Т.е. радиус = СД/2=10/2=5
АВ=CD = 9см, ВС =AD = 15см.
Объяснение:
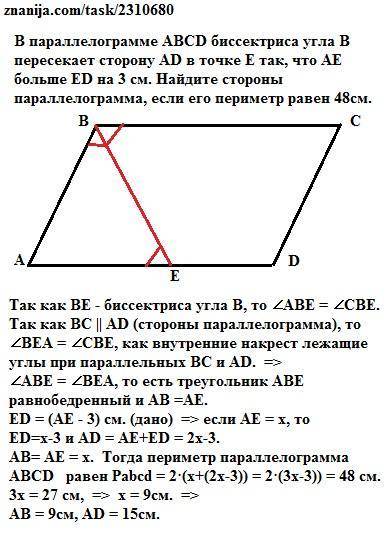
Так как ВЕ - биссектриса угла В, то ∠АВЕ = ∠СВЕ.
Так как ВС || AD (стороны параллелограмма), то
∠ВЕА = ∠СВЕ, как внутренние накрест лежащие углы при параллельных ВС и AD. =>
∠АВЕ = ∠ВЕА, то есть треугольник АВЕ равнобедренный и АВ =АЕ.
ЕD = (АЕ - 3) см. (дано) => если АЕ = х, то
ED=х-3 и AD = АЕ+ED = 2х-3.
АВ= АЕ = х. Тогда периметр параллелограмма ABCD равен Рabcd = 2·(х+(2х-3)) = 2·(3х-3)) = 48 см.
3х = 27 см, => х = 9см. =>
АВ = 9см, AD = 15см.
Противоположные стороны параллелограмма равны =>
AB=CD, BC=AD.
Объяснение:Угол COA=180-120=60°
CO=CD/2=14/2=7cm
OA=OC
AC²=OC²+OA²-(2*OC*OA*cos(60°))=
=49+49-(2*7*7*1/2)=98-49=49
AC=√49=7 cm