Пусть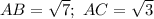 
. Из условия AE = BC, а так как
AM - медиана треугольника ABC, то BE = EC = BC/2 = AE/2.
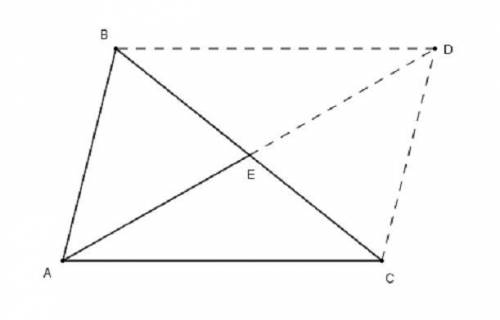
Сделаем дополнительное построение, т.е. построим до параллелограмма ABDC, в нём AD = 2AE = 2BC, тогда сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
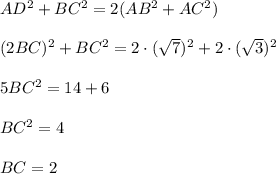
Не трудно заметить, что треугольник ABC - прямоугольный с гипотенузой AB = √7 и катетами AC = √3; BC = 2.
2) Площадь треугольника: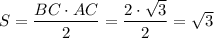 
кв. ед.
3) Центр описанной окружности лежит на середине гипотенузы, значит радиус описанной окружности равен половине гипотенузы.
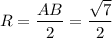
ответ:4)а 5)в 6)б 7)в
Объяснение:4)Т.к центральный угол О =100°=> и дуга, на которую он смотрит тоже равна 100°,тогда х=50,потому что он вписаный(вписаный угол равен половине дуги ,на которую он опирается)
5)угол равен 70,тогда дуга равна 140(описанный угол,дуга в 2р больше него)
Вся окружность =360
360-140=220(это дуга,на которую смотрит х),тогда сам х=220:2=110(угол вписанный)
6)О=64,дуга тоже 64(центральный),х описанный =64/2=32
7)Т.к ВО(это радиус)=АД,то АД=ДО т.к ДО тоже радиус,тогда ВО в 2р меньше ВО,угол В=90 т.к радиус ,проведенный в точку касания явл. перпендикуляром на эту касательную.Тогда мы можем применить свойство треугольника :сторона,лежащая напротив угла в 30°=половине гипотенузы ,тогда угол ВАО=30,а ВАО=ОВС т.к это касательные вышли из 1ой точки,тогда угол ВАС=60