
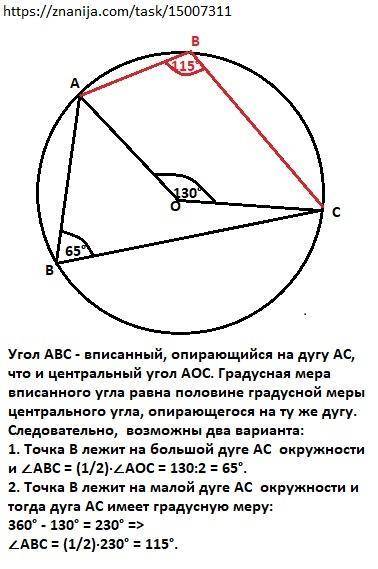
1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
Угол MON равен углу ONK, так как они внутренние накрест лежащие.
МО = ОК = ON, так как от центра окружности, до её края расстояние под любым углом будет одинаково.
Рассмотрим треугольник ONK образованный в окружности :
Если ОК = ON, то треугольник равноьедренный, а значит углы при основании равны.
N = К = 56°
Рассматривая общую картину :
Угол MKN = 56°