Объяснение:
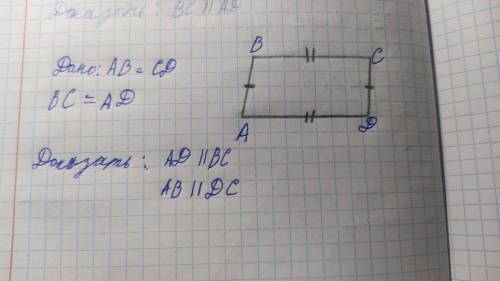
АВСД параллелограмм (противоположные стороны попарно равны: определение). В параллелограмме противоположные стороны параллельны (свойство). Следовательно АВ║СД и ВС║АД.
Рассмотрим две пересекающиеся в точке M прямые a и b. Через две пересекающиеся прямые можно провести плоскость, назовем её P.
Проведем прямую c, которая пересекает прямые a и b в точках A и B соответственно.
A принадлежит a -> A принадлежит P
B принадлежит b -> B принадлежит P
-> прямая c лежит в плоскости P
с - произвольная прямая -> все прямые, которые пересекают a и b и не проходят через M - точку пересечения прямых a и b лежат с этими прямыми в одной плоскости.
Теперь рассмотрим случай, когда прямые проходят через точку пересечения M прямых a и b.
Возьмем произвольную точку N, которая не лежит в плоскости P и проведем прямую через точки N и M.
Прямая NM не принадлежит плоскости P.
Итак, основной вывод.
Прямые, которые пересекают две пересекающиеся прямые и не проходят через их точку пересечения всегда лежат с этими прямыми в одной плоскости.
Те прямые, которые проходят через точку пересечения пересекающихся прямых не всегда лежат с ними в одной плоскости.
Проводим BD
1. Рассмотрим ΔABD и ΔBDC
1) BD -- общая
2) AB = CD (по усл.)
3) AD = BC (по усл.)
Следовательно, ΔABD = ΔBDC (по 3 признаку)
2. ΔABD = ΔBDC ⇒ ∠ABD = ∠BDC и ∠CBD = ∠BDA (соотв. элементы равных треугольников)
3. ∠ABD = ∠BDC -- накр. леж. при прямых AB и CD и секущей BD ⇒ AB || CD (по признаку параллельности прямых)
∠CBD = ∠BDA -- накр. леж. при прямых BC и AD и секущей BD ⇒ BC || AD (по признаку параллельности прямых)
ч. т. д.