если А (2;-3) и b (-2;5)
Объяснение:
,тогда все другие прямые лежат с ней в одной плоскости(аксиома) теперь среди оставшихся прямых выберем прямую 
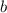.Она лежит с прямой в одной плоскости.Но другие прямые тоже лежат с прямой 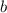в одной плоскости(та же аксиома) и они же лежат в одной плоскости с прямой . по аксиоме плоскость определяется однозначно по двум пересекающимся прямым.Следовательно все оставшиеся прямые ,которые пересекаются и с и с 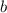лежат в плоскости ,образованной при пересечении и 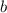. Значит все прямые лежат в одной плоскости
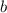,тогда все другие прямые лежат с ней в одной плоскости(аксиома) теперь среди оставшихся прямых выберем прямую .Она лежит с прямой в одной плоскости.Но другие прямые тоже лежат с прямой 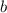в одной плоскости(та же аксиома) и они же лежат в одной плоскости с прямой . по аксиоме плоскость определяется однозначно по двум пересекающимся прямым.Следовательно все оставшиеся прямые ,которые пересекаются и с и с 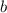лежат в плоскости ,образованной при пересечении и 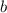. Значит все прямые лежат в одной плоскости
Дано:
Диаметр окружности: отрезок .
Центр окружности: точка .
Координаты следующих точек: .
Найти нужно координаты центра окружности: .
Найдём координаты центра окружности, используя правило нахождения среднего арифметического чисел.
Т.е. возьмём у точки "A" и точки "B" координату по оси абсцисс (Ox). Представьте, что мы должны найти среднее арифметическое чисел "6" и "-2".
Вспоминаем правило: чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество (пример прикреплён ниже).
Теперь поработаем с выбранными координатами точек:
.
Теперь мы знаем, что за координата указана по оси абсцисс. Но нам ещё нужно найти координату по оси ординат (Oy).
Делаем всё по аналогии нахождения координаты оси абсцисс. Берём вторые координаты у обоих точек, которые образуют отрезок "AB". Это будут координаты "-7" и "5". Теперь находим их среднее арифметическое и получаем ответ:
.
(чертёж к задаче прикреплён ниже)
ответ: https://tex.z-dn.net/?f=%5CLarge%20%7B%20%5Cboxed%20%7B%20%5Cbold%20%7B%20O(2%3B%20%5C%3A%20-1)%7D%7D%20%7D
.