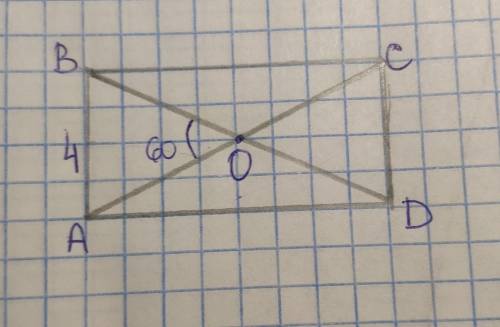
Дано:
АВCD – параллелограмм;
АС=BD;
Угол АОВ=60°
АВ=4
Найти:
S(ABCD)
Диагонали параллелограмма точкой пересечения деляться пополам, тогда ВО=0,5*BD; АО=0,5*AC
AC=BD по условию, следовательно 0,5*АС=0,5*BD.
Следовательно ВО=АО, значит ∆АОВ – равнобедренный с основанием АВ.
Углы при основании равнобедренного треугольника равны, тогда угол ABO=(180°–угол AOB)÷2=(180°–60°)÷2=60°.
Если диагонали параллелограмма равны, то такой параллелограмм – прямоугольник. То есть АВCD – прямоугольник.
Следовательно угол BAD=90° как угол прямоугольника. Тогда ∆ABD – прямоугольный.
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно угол ADB=90°–угол АОD=90°–60°=30°.
В прямоугольном треугольнике против угла в 30° лежит катет, вдвое меньший гипотенузы. То есть
AB=0,5*BD
BD=2*AB=2*4=8
По теореме Пифагора в прямоугольном ∆ABD:
BD²=AB²+AD²
AD²=BD²–AB²
AD²=8²–4²
AD²=64–16
Совокупность:
AD=√48
AD=–√48
Совокупность:
AD=4√3
AD=–4√3
Так как длина задаётся положительным числом, то AD=–4√3 не может быть.
Следовательно AD=4√3.
S=а*b,
где S – площадь прямоугольника, а и b – смежные стороны.
S=AB*AD=4*4√3=16√3
ответ: 16√3
ответ:Треугольник ЕDF согласно условию является равнобедренным,и по определению его боковые стороны равны между собой и равны углы при основании.
Если из вершины D на основание ЕF мы опустим перпендикуляр,а это и медиана и биссектриса,то получим два прямоугольных треугольника,которые равны между собой по третьему признаку равенства треугольников
ЕD=DF по условию ,как боковые стороны равнобедренного треугольника
EA=AF,т к DA медиана и она поделила основание треугольника ЕF на два равных отрезка
DA-общая сторона
Рассмотрим треугольник ЕDA
<DAE=90 градусов,т к DA высота и опущена на основание перпендикулярно
Зная гипотенузу треугольника DE (12 cм) и катет (5:2=2,5 см) вычислим углы треугольника
<E=78 градусов
<ЕDA=12 градусов
Т к DA является и биссектрисой угла D,то <D=12+12=24 градуса
Так как <Е=<F, то и <F=78 градусов
Проверка
78+78+24=180 градусов
ответы на вопросы
1.Угол D меньше суммы углов при основании E и F
2.Угол D не больше суммы углов при основании Е и F
3.Угол D не больше угла Е и не больше угла F
4.Угол D меньше угла Е и меньше угла F
Объяснение: