60√3 см^2
Объяснение:
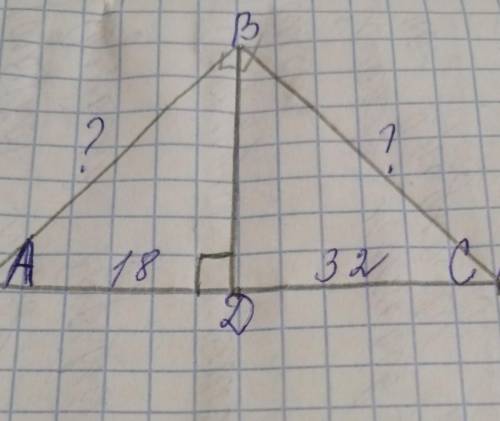
назвемо трапецію ABCD
S =
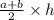
, де S - площа трапеції, a,b - основи, h - висота проведена до основи.
проведемо висоту. назвемо її ВК.
Розглянемо трикутник АВК.
кут К = 90°, отже трикутник прямокутний.
кут А = 60°, за умовою.
за формулою суми кутів трикутника, маємо:
кут В = 180° - 90° - 60° = 30°
за теоремою катета проти кута 30°, маємо:
АК = 12/2 = 6 (см)
знайдемо ВК. за теоремою Піфагора, маємо:
ВК^2 = АВ^2 - АК^2.
ВК^2 = 144 - 36 = 108
ВК = √108 = 6√3
тепер, знайдемо більшу основу.
4+6+6= 16 (см)
підставляємо у формулу:
(4 + 16)/2 × 6√3 = 60√3 (см^2).
ABCDA1B1C1D1-куб, АВ=1. Вычислите : (АВ+ВС)*ВВ1 ( последние буквы это векторы)
Объяснение:
Найти скалярное произведение векторов (АВ+ВС)*ВВ₁ .
(АВ+ВС)*ВВ₁ =АС*ВВ₁ .
Вектора АС и ВВ₁ перпендикулярны, т. к боковые ребра перпендикулярны плоскости основания⇒скалярное произведение равно 0
По определению скалярного произведения
АС*ВВ₁ =|АС|*|ВВ₁|cos( АС,ВВ₁ )
|АС|-это длина диагонали . Из ΔАВС по т. Пифагора √2
|ВВ₁|=1 это сторона квадрата..
Угол между АС и ВВ₁ равен 90°, тк. боковые ребра перпендикулярны плоскости основания.
АС*ВВ₁ =√2*1* cos90=√2*1*0=0