Объяснение:
1)Рассмотрим треугольник ABC
2) Т.к. треугольник ABC прямоугольный,→ гипотенуза равна двум катетам, лежащих напротив острого угла величиной в 30°,т.к. ∠B=30°. → BC=2*AC,→ BC=2*14=28см
ответ: гипотенуза BC=28см

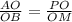
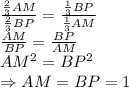
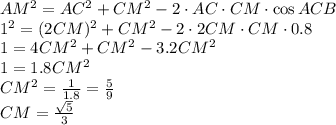
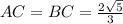
1)описанной
2)вписанным
3)около него
4)описать
5)Г
6)Одну
7)Г
8)В
Объяснение:
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около этого многоугольника, а многоугольник вписанным в эту окружность.
Если сумма противоположных углов четырехугольника равна 180, то около него можно описать окружность.
Около любого треугольника можно описать окружность(вариант г)
Около треугольника можно описать только ОДНУ окружность.
Центром описанной около треугольника окружности является точка пересечения:г
Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:
в)
28
Объяснение:
14*2=28 см