ответ:Номер 1
Трапецию в тетради начерти сам
Номер 2
Если вписанный угол и центральный угол опираются на одну и ту же дугу,то вписанный угол всегда в два раза меньше центрального
Вписанный угол равен
90:2=45 градусов
Номер 3
Если четырёхугольник вписан в окружность,то его противоположные углы в сумме должны составлять 180 градусов
<С=105 градусов. <А=180-105=75 градусов
<D=60 градусов. <В=180-60=120 градусов
Номер
Средние линии равны половине основных сторон
14:2=7см
12:2=6 см
18:2=9 см
Р=7+6+9=22 см
Можно было сделать проще,узнать периметр основного треугольника и разделить его на 2
Р=(14+12+18):2=44:2=22 см
Объяснение:
Sabcd = 67,62 cм²
Объяснение:
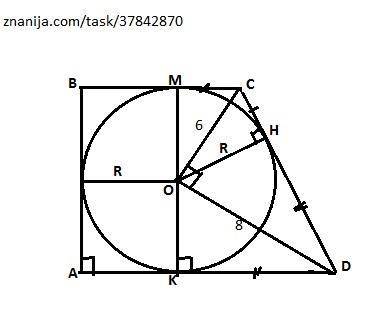
Боковая сторона описанной трапеции видна по углом 90° (свойство). Следовательно, треугольник СОD прямоугольный и его высота ОН, проведенная к гипотенузе CD, является радиусом вписанной окружности. Высота нашей трапеции равна двум таким радиусам. Тогда по Пифагору CD = √(OC²+OD²) = √36+64) = 10 cм.
По свойству высоты из прямого угла:
ОН = R = (OC·OD)/CD = 6·8/10 = 4,8 см.
Также по свойству этой высоты:
ОС² = СD·CH => CH = OC²/CD = 36/10 = 3,6 см.
Аналогично HD = OD²/CD = 6,4 cм.
Пусть точки М и К - точки касания вписанной окружности с основаниями трапеции ВС и AD соответственно.
Тогда ВМ = АК = R = 4,8 см.
МС = СН = 3,6 см, а KD = HD = 6,4см (как отрезки касательных из одной точки).
ВС= ВМ+МС = 4,8+3,6 = 8,4 см.
AD = AK+KD = 4,8+6,4 = 11,2 cм.
Sabcd = (BC+AD)·MK/2 = 19,6·9,6/2 = 67,62 см²
Є кілька ів.
Покажу один з них.
Рішення та малюнок на фото.
Висоти трапецій подібні, отже і площі також подібні.
Відповідь: 108 см²