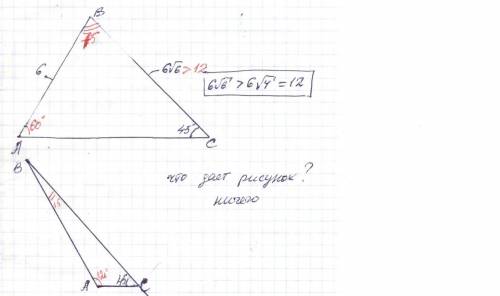
Найдите углы A и B треугольника ABC, если AB=12 см, BC=6√6 см, угол C= 45°.
ответ: 60° , 75° или 120° , 15° .
Объяснение:
По теореме синусов : BC / sin(∠A) =AB / sin(∠C ) ⇔
6√6/sin(∠A)=12/sin45°⇔sin(∠A) =6√6*sin45°/12=6√6 *(√2/2) / 12 = 3 /2 ⇒
∠A= 60° или ∠A= 120° . Оба верны ∠A > ∠C , т.к. BC > AB
( в треугольнике против большой стороны лежит большой угол )
* * * BC > AB : BC = 6√6 > 6√4 = 12 = AB * * *
∠B = 180° - (∠A+√C) → ∠B = 75° или ∠B = 15° см. лишнее приложение
Объяснение:
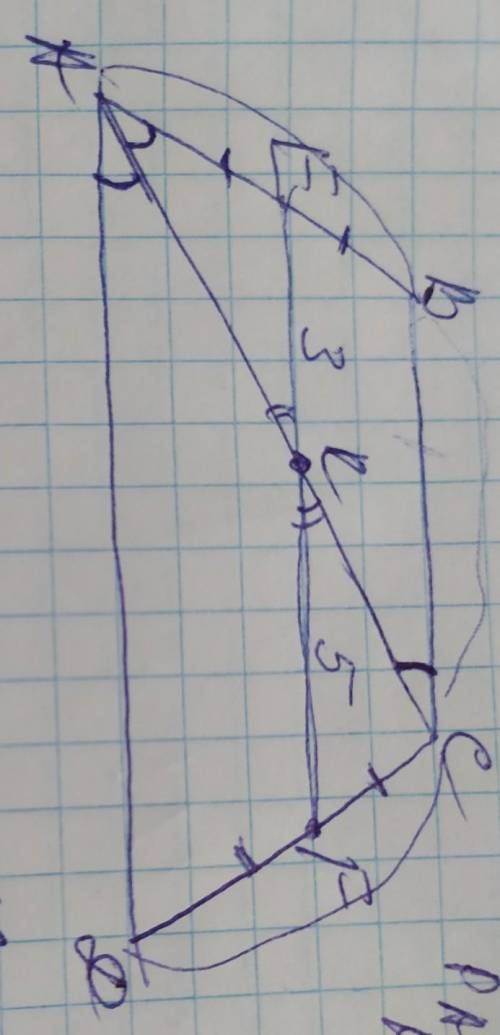
диагональ АС делит трапецию на 2 треугольника: АВС и АСД. Рассмотрим полученный ∆АСД. Так как точка Е - середина отрезка АВ, то точка F будет середина отрезка СД, следовательно EF является средней линией трапеции. Тогда KF будет являться средней линией ∆АСД (по теореме Фалеса: если прямая отсекает равные отрезки на одной стороне угла, то она отсекает равные отрезки и с другой стороны этого угла). По правилу треугольника его средняя линия=½ его основания, поэтому КF=½АД, или АД=2KF=5×2=10см
Если ЕF средняя линия трапеции, то она составит:
EK+KF=3+5=8см. Средняя линия трапеции вычисляется по формуле:
(ВС+АД)/2=EF. Используя эту формулу найдём сторону ВС:
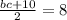
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
ВС+10=8×2
ВС+10=16
ВС=16–10=6см
Рассмотрим ∆АВС. В нём <ВАС=<САД, поскольку диагональ АС биссектриса угла А. Так как ВС||АД, то <САД=<ВСА как внутренние разносторонние поэтому <ВАС=<ВСА, следовательно ∆АВС равнобедренный и АВ=ВС. Поскольку трапеция равнобедренная, то АВ=СД=ВС=6см
Теперь найдём периметр трапеции зная её стороны:
Р=АВ+ВС+СД+АД=6×3+10=18+10=28см
ОТВЕТ: Р=28 см