Доказательство:
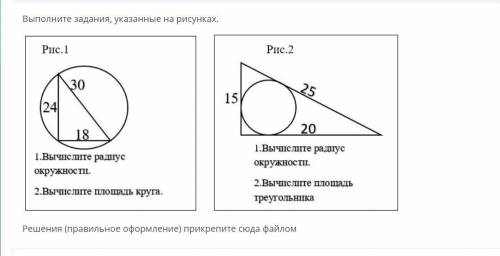
Смотри прикреплённый рисунок.
АВ - диаметр окружности с центром в точке О.
СK = DK - половинки хорды CD.
К - точка пересечения АВ и CD
Соединим концы хорды С и D с центром окружности О.
ΔСОК = Δ DOK по 3-му признаку (СK = DK по условию, ОС = ОD - радиусы окружности, ОК - общая сторона)
Следовательно, ∠СКО = ∠DKO.
Эти углы в сумме составляют развёрнутый ∠СКD = 180°
Следовательно, ∠СКО = ∠DKO = 0,5 ∠СКD = 0,5 · 180° = 90°.
Доказано, что ОК ⊥ CD.
Так как ОК является частью диаметра АВ, то АВ ⊥ CD, что и требовалось доказать.
Если угол В = 45гр, то поскольку ΔАВС прямоугольный, то второй уострый угол его угол А = 45гр. Тогда ΔАВС равнобедренный и ВС = АС = 2а.
Поскольку АМ = СМ, а ЕМ перпендикулярно АС, то ЕМ параллельно ВС и ЕМ - средняя линия ΔАВС и ЕМ = 0,5ВС = а
В ΔАСД угол Д прямой, АС - гипотенуза, а угол АСД = 60гр. Следовательно угол САД = 30гр. А катет СД, лежащий против угла в 30 гр., равен половине гипотенузы АС, т.е. СД = АС : 2 = а
Таким образом ЕМ = а и СД = а, т.е. ЕМ = СД, что и требовалось доказать.