№1:  . №2:
. №2: 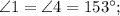
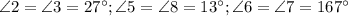 .
.
№1.
Пусть  , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна  .
.
 , по условию.
, по условию.
 и
и  - односторонние углы
- односторонние углы 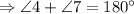
№2.
Обозначим данные прямые буквами 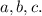
Пусть  - секущая прямых
- секущая прямых  и
и 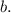
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
 и
и 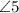 - накрест лежащие при пересечении
- накрест лежащие при пересечении  и
и  секущей
секущей  , однако
, однако 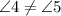 .
.

 и
и  - не параллельны.
- не параллельны.
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна  ".
".
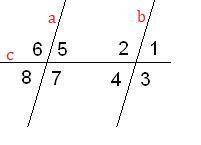
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и 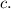
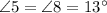 , по свойству вертикальных углов.
, по свойству вертикальных углов.
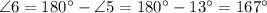 , по свойству смежных углов.
, по свойству смежных углов.
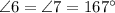 , по свойству вертикальных углов.
, по свойству вертикальных углов.
===========================================================
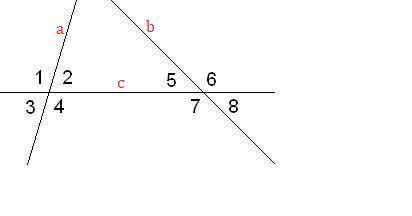
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и  .
.
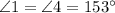 , по свойству вертикальных углов.
, по свойству вертикальных углов.
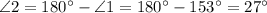 , по свойству смежных углов.
, по свойству смежных углов.
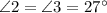 , по свойству вертикальных углов.
, по свойству вертикальных углов.
Пусть координаты С(х;у)
1) λ=1 значит, что АС=СВ и С-середина отрезка.
С( (2-1):2 ;(3+2):2 ) , С( 0,5 ; 2,5);
2) λ = 1/2
х=(х₁+λх₂):(1+λ) , у=( у₁+λу₂):(1+λ;
х=(2+1/2*(-1)):(1+1/2) , у=(3+1/2*2):(1+1/2)
х= 1,5: 1,5 , у=4 :1,5
х=1 , у= 2 \frac{2}{3}232
С(1 ; 2 \frac{2}{3}232 ).
х=(х₁+λх₂):(1+λ) ,у=( у₁+λу₂):(1+λ) ,где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у)-координаты точки, делящей отрезок в заданном отношении.