Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
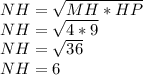
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
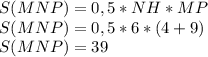
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
Объяснение:
центральный угол равен внутреннему равен 90 градусов для квадрата
центральный угол равен 120 градусов и больше чем внутренний угол равностороннего треугольника равного 60 градусов
вроде определились что это треугольник но надо доказать что это именно то что нам нужно
центральный угол правильного n - угольника равен 360/n
внутренний угол правильного n - угольника равен 180*(n-2)/n
по условию 360/n = 2 * 180*(n-2)/n
отсюда следует n-2 = 1
n = 3 - значит это треугольник
периметр искомого треугольника равен 3*2 см = 6 см