1) пусть x - это катет в левой части трапеции с острым углом 30°
пусть y - это катет в правой части трапеции с острым углом 60°
на них приходится 15 - 7 = 8см, следовательно, x + y = 8
выясним, как связаны x и y
tg60 = h / y => y = h / tg60 = h / √3
tg30 = h / x => x = h / tg30 = 3h / √3
заметим, что x > y в 3 раза
пусть x = 3a, y = a
тогда 3a + a = 8,
a = 2
следовательно, x = 6, y = 2
теперь через тот же тангенс найдем высоту трапеции:
tg60 = h / y => h = tg60 y = 2√3.
2) по теореме Пифагора найдем диагонали трапеции
d1 = sqrt(9² + (2√3)²) = √93
d2 = sqrt(13² + (2√3)²) = √181
Объяснение:
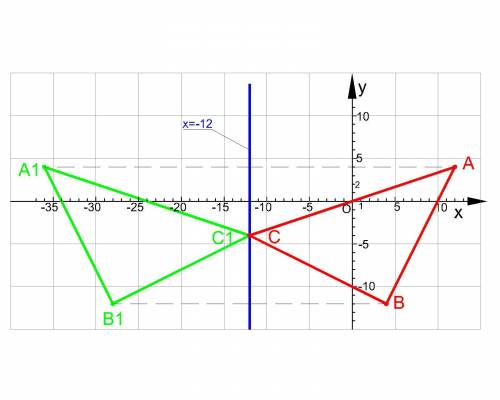
1. Выполняем построение треугольника АВС.
2. Строим график прямой х = -12 . Это вертикальная прямая проходящая через точку (-12; 0)
3. Выполняем построение симметричной фигуры:
от т. А проводим перпендикуляр к прямой х = -12. Откладываем перпендикуляр такой же длины в противоположною сторону от х = -12.
То же самое выполняем для т. В. Т. С совпадает с точкой С1, т.к. абсцисса т. С = -12 и лежит на прямой х = -12.
Координаты ΔA1B1C1 можно определить графически:
А1(-36;4) , В1(-28; -12) , С1(-12; -4).
Также абсциссы можем определить математически:
х1 = -12 - (12+х) = -24-х.
Здесь -12 - это сдвиг координат влево на 12 единиц, (12+х) расстояние между осью симметрии и точками исходного треугольника.
Ординаты остаются неизменными, т.к. ось симметрии - вертикальная.
cos 64°= 6/AB
0,638=6/AB
AB≈9 см
За т. Піфагора
АС²=9²-6²
АС²=81-36
АС=√45=3√5
В: 9; 3√5