В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.
Трапеция - четырехугольник, и, поскольку в нее вписана окружность, сумма оснований равна сумме ее боковых сторон.
В равнобедренной трапеции высота делит большее основание на два отрезка, из которых больший равен полусумме оснований, а меньший - их полуразности.
Периметр трапеции АВСД равен р
Следовательно,
сумма боковых сторон равна р:2,
сумма оснований равна р:2.
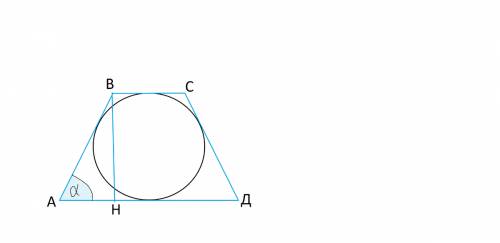
Опустим высоту ВН.
Отрезок НД большего основания равен полусумме оснований и равен (р:2):2=р:4
Боковая сторона АВ равна половине полупериметра трапеции и равна
(р:2):2=р:4
Из прямоугольного треугольника АВН найдем высоту ВН:
ВН=АВ·sin (α)=(р:4)·sin (α)=(р·sin α):4
Площадь трапеции равна произведению высоты на полусумму оснований.
S АВСД=ВН·НД=(р:4)(р·sin (α):4)=(р²·sin α):16 ( единиц площади)
Площадь круга, вписанного в эту трапецию, находим по формуле
S=πr²
Высота трапеции - диаметр этого круга.
Соответственно, его радиус - половина высоты трапеции,
r= ВН:2=(р·sin α):8
а площадь
S= π·{р·sinα }²:64 ( единиц площади).
1.) Радиус цилиндра 2 см, а диагональ осевого сечения 5 см. Найдите:
a) Высоту цилиндра
Прямоугольный треугольник. Т. Пифагора
Н² = 5² - 4² = 9, ⇒ Н = 3
б) Площадь осевого сечения
Осевое сечение - прямоугольник
S = 3*4 = 12
в) Диаметр основания
Диаметр основания = 2 радиуса = 4
2.) Образующая конуса равна 6 м и наклонена к плоскости основания под углом 60 градусов. Найдите площадь основания конуса, площадь осевого сечения.
Прямоугольный треугольник. Гипотенуза = 6, катет = радиусу лежит против угла 30, значит, R = 3
высота конуса = √(36 - 9) = √27 = 3√3
площадь основания конуса = S кр = πR² = π*9= 9π
Осевое сечение = треугольник, котором боковые стороны = 6, основание = 6 и высота = 3√3
S = 1/2*6*6*3√3 = 54√3
3.) Найдите площадь большого круга и длину экватора шара, если его радиус 2 м.
S= πR² = π*4 = 4π(м²)
C = 2πR = 2π*2 = 4π(м)