1) Если площадь равностороннего треугольника равна 0,5a, то длина катетера равна..
2) Рассчитайте длину гипотенузы, если известно, что разница между катетерами составляет 3 см, а узкий угол - 60 °!
3) Вычислите длины сторон равностороннего треугольника, если их угол составляет 60°, а площадь треугольника составляет 16 V3 см!
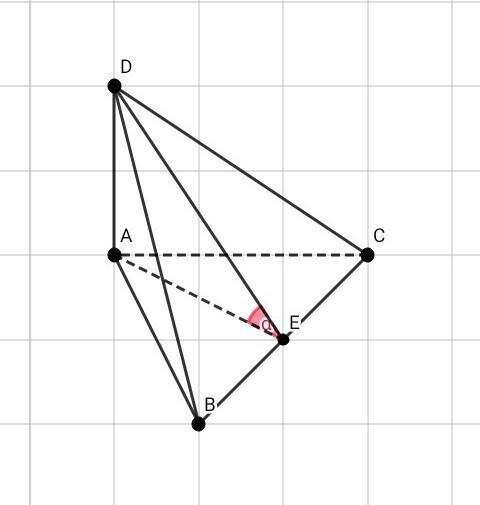
В ∆ АВС опустим высоту АЕ перпендикулярно BC, тогда
DA перпендикулярен ( ABC )
AE принадлежит ( АВС )
Значит, DA перпендикулярен AE
AE перпендикулярен ВС
Тогда по теореме о трёх перпендикулярах DE перпендикулярен ВС
Из этого следует, что угол AED – линейный угол двугранного угла ABCD.
Рассмотрим ∆ АВС:
Высота равностороннего треугольника вычисляется по формуле:
h = a√3 / 2
где а – сторона равностороннего треугольника, h – высота
AE = AB × √3 / 2 = 6 × √3 / 2 = 3√3
Рассмотрим ∆ AED (угол DAE = 90°):
tg AED = AD / AE = 4 / 3√3 = 4√3 / 9
ОТВЕТ: 4√3 / 9