пусть ad> bc , тогда острые углы равные 75 и 15 гр лежат при оснований ad , положим что y,w середины сторон ab и cd соответственно , тогда yw средняя линия трапеции , значит ad+bc=2yw из условия мы знаем что yw равна либо 15 либо 7 , положим что ab и cd пересекаются в точке e , тогда aed=180-(75+15)=90 , положим также что z,x это середины сторон основании bc,ad соотвественно , пусть n точка пересечения yw и zx , тогда по замечательному свойству трапеции точки e,z,x лежат на одной прямой , учитывая что угол aed прямой , получаем что ax=ex=ad/2 , ez=bz=bc/2 , но так как ex=ez+zx откуда окончательно получаем две системы
{ad-bc=2*7
{ad+bc=2*15
или
{ad-bc=2*15
{ad+bc=2*7
подходит решение первой системы , так как они положительны , складывая получаем ad=22 , bc=8 , значит ответ bc=8.
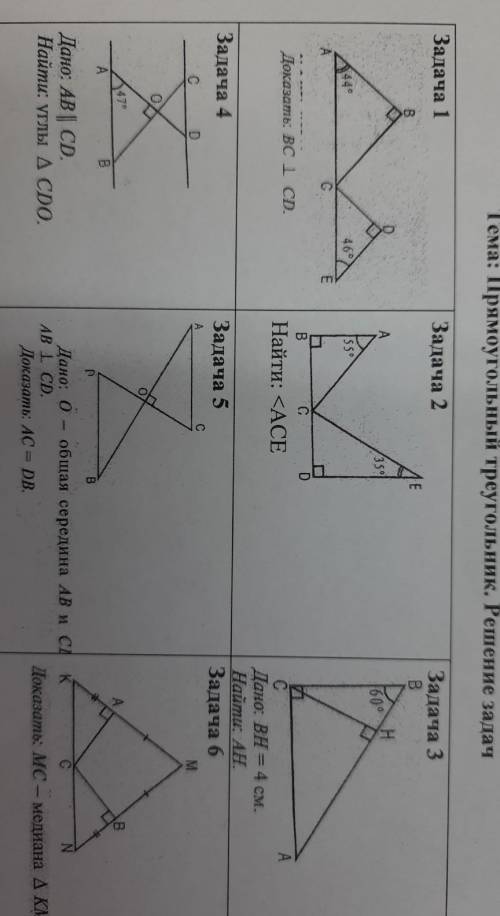
ответ: 90°; 12 см; ∠COD=90°; ∠ОСD=43°; ∠ОDС=47°
Объяснение: 2) треугольники АВС и СDE прямоугольные ∠АСВ=90-55=35°.
∠ECD=90-35=55°
∠АСЕ развернутый и равен 180°
Значит ∠АСЕ=∠ВСD-∠ЕСD-∠АСВ=180-35-55=90°
3) ∠СВH=60°. Значит ∠ВСH=90-60=30°
BH лежит против угла 30° и является катетом ΔСBH. ВС гипотенуза в это треугольнике. Значит ВС=ВH*2=4*2=8 cм.
∠САВ тоже 30° и СВ летит против угла 30°. Значит АС=ВС*2=8*2=16 см. АH=АВ-ВH=16-4=12 cм
4) ∠ВАО=∠СD0=47°, как накрест лежащие при пересечении параллельных прямых секущей.
∠АОВ=∠СОD=90°, как вертикальных углы.
Значит ∠АВО=∠ОСD=90-47=43°