Теорема d3. В равнобедренном треугольнике высоты, опущенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его высоты. Тогда углы ABL и KAB равны, так как углы ALB и AKB прямые, а углы LAB и ABK равны как углы при основании равнобедренного треугольника. Следовательно, треугольники ALB и AKB равны по второму признаку равенства треугольников: у них общая сторона AB, углы KAB и LBA равны по вышесказанному, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Если треугольники равны, их стороны AK и BL тоже равны.
ЧТД
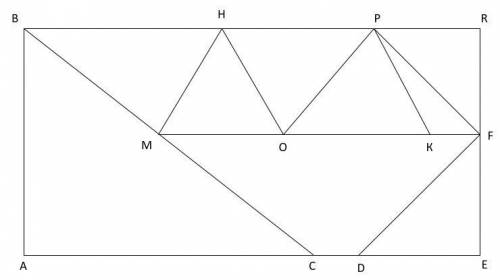
ответ: BMH : прямоугольный, разносторонний
PKF : остроугольный, разносторонний
MHO : правильный.
PRF : равнобёдренный, прямоугольный.
FED : равнобёдренный, прямоугольный
HOP : разносторонний, остроугольный.
ABC : прямоугольный, разносторонний
OPF : прямоугольный, равнобёдреный
OPK : разносторонний , остроугольный