Объяснение:
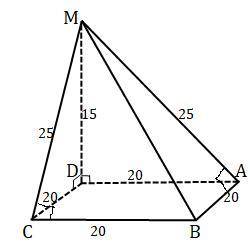
S(бок)= S(МDА)+S(МDС)+S(МАВ)+S(МСВ)
1)Т.к. МD⊥(АВС) , то МD⊥DА , МD⊥DС.
Δ МDА= МDС как прямоугольные по 2-м катетам : МD-общая, АD=DС как стороны квадрата , S(МDА)=S(МDС)=1/2*20*15=150(см²).
2) МD⊥( АВС), DА⊥АВ , значит МА⊥АВ по т. о 3-х перпендикулярах⇒ΔМАВ-прямоугольный.
МD⊥( АВС), DС⊥СВ , значит МС⊥СВ по т. о 3-х перпендикулярах⇒ΔМСВ-прямоугольный.
3) ΔМАВ= ΔМСВ, как прямоугольные по катетам МА=МС=25 и общей гипотенузе МВ. Поэтому S(МАВ)=S(МСВ)=1/2*20*25=250 (см²).
4)S(бок)= 2*150+2*250=800 (см²).
В этом легко наглядно добиться, если нарисовать окружность и принять диаметр в ней за гипотенузу. Любой треугольник в этой окружности с имеющейся гипотенузой и катетами, проведёнными к любой точке окружности будет прямоугольным, так ка вписанный угол опирается на дугу в 180°.
Очевидно, что высоты эти тр-ков будут разными, но наибольшая высота будет равна радиусу окружности, то есть половине гипотенузы. h=√((c/2)·(c/2))=√(c²/4)=c/2.