Дано :
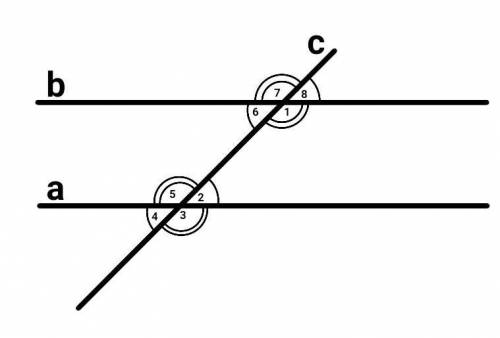
a || b.
c - секущая.
<1 = 129°.
Найти :
<2 = ?
<3 = ?
<4 = ?
<5 = ?
<6 = ?
<7 = ?
<8 = ?
При пересечении двух параллельных прямых секущей накрест лежащие углы равны, соответственные углы равны, сумма односторонних углов равна 180°.<1 и <2 — односторонние.
По выше сказанному —
<1 + <2 = 180°
<2 = 180° - <1 = 180° - 129° = 51°.
<2 = <6 = 51° — как накрест лежащие при параллельных прямых
<1 = <3 = 129° — как соответственные при параллельных прямых
<2 = <8 = 51° — как соответственные при параллельных прямых
<2 = <4 = 51° — как вертикальные
<1 = <7 = 129° — как вертикальные
<1 = <5 = 129° — как накрест лежащие при параллельных прямых
51°, 129°, 51°, 129°, 51°, 129°, 51°.
сделаем построение по условию
дополнительно
параллельный перенос прямой (BD) в прямую (B1D1)
искомый угол <AB1D1 в треугольнике ∆AB1D1
по теореме Пифагора
AB1=√(a^2+(3a)^2) =a√(1+9)= a√10
B1D1=√(a^2+(2a)^2) =a√(1+4)= a√5
AD1=√((2a)^2+(3a)^2) =a√(4+9)= a√13
по теореме косинусов
AD1^2 = AB1^2+B1D1^2 - 2*AB1*B1D1 * cos<AB1D1
(a√13)^2=(a√10)^2 + (a√5)^2 - 2* a√10* a√5 * cos<AB1D1
13a^2=10a^2 + 5a^2 -10√2a^2 * cos<AB1D1
cos<AB1D1 = 13a^2-(10a^2 + 5a^2) / -10√2a^2 = -2a^2 / -10√2a^2 = √2/10
<AB1D1 = arccos (√2/10)
ответ угол между прямыми BD AB1 arccos (√2/10)