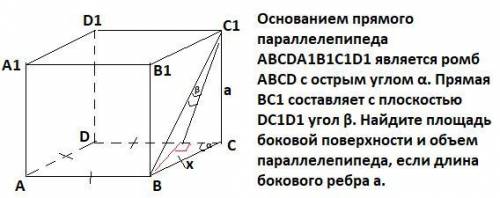
Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб АВСD с острым углом α. Прямая BC1 составляет с плоскостью DC1D1 угол β. Найдите площадь боковой поверхности и объем параллелепипеда, если длина бокового ребра а.
Объяснение:
S(бок)=Р*L, V=S(осн.)*L ,где L-боковое ребро , перпендикулярное плоскости основания.
Пусть сторона ромба х , ∠DCB=α , ВН⊥DC. Тогда углом между плоскостью (DC₁D₁) и прямой ВС₁ будет ∠ВНС₁=β .
ΔВНС-прямоугольный , ВН=х*sinα.
ΔBHC₁-прямоугольный , ВН=ВС₁*sinβ .
ΔBCC₁ прямоугольный ,BC₁=√(x²+a²), поэтому
ВН=√(x²+a²)*sinβ . Приравняем правые части для ВН и найдем сторону ромба.
х*sinα=√(x²+a²)*sinβ , х²*sin²α=(x²+a²)*sin²β , х²*sin²α-x²*sin²β=a²*sin²β , х²*(sin²α-sin²β)=a²*sin²β , х=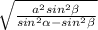
, x=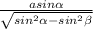
.
S(бок)=4а* 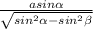, S(бок)=
.
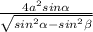V=а²sinα*а=а³sinα
==============
Угол между прямой и плоскостью .это угол между основанием перпендикуляра и основанием наклонной.
Объяснение:
vijohi8766
хорошист
20 ответов
2.9 тыс. пользователей, получивших
Смотри аналог с описанием решения (Если будет что-то не понятно, то пиши мне ❤️)
Объяснение:
Известна формула нахождения координат середины отрезка по координатам его концов:
xc = (xa + xb)/2, yc = (ya + yb)/2, где (xc; yc) – координаты точки С, которая является серединой отрезка AB.
В нашем примере даны координаты одного конца и середины отрезка. Воспользовавшись выше приведенной формулой преобразуем его для вычисления второго конца отрезка:
Xc = 2xb - xa, yc = 2yb - ya; xc = 2 * 6 - 6 = 6, yc = 2 * 6 – 4 = 8. C(6; 8).
Точка D — середина отрезка BC, поэтому xd = (xc + xb)/2, yd = (yc + yb)/2;
xd = (6 + 6)/2, yd = (8 + 6)/2; xd = 6, yd = 7. D(6;7).
ответ: C(6; 8); D(6;7).
сумма углов прилегающих к одной стороне=180
угол1=х, угол2=2х, х+2х=180, х=60, 2х=120