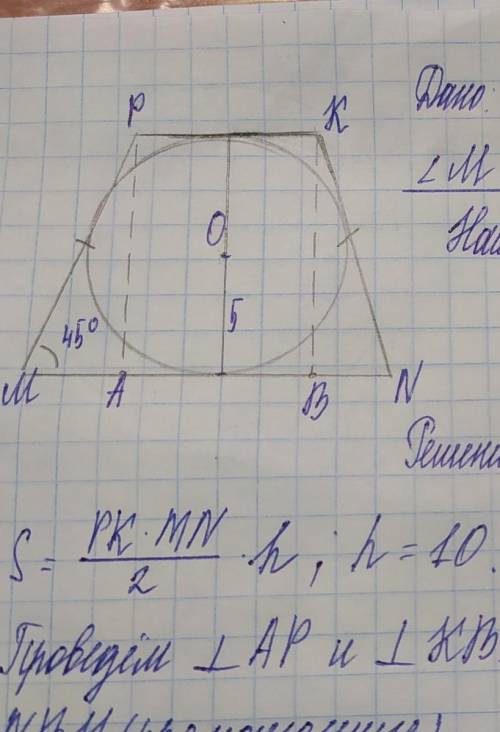
8) Объем конуса равен: V=1/3пR^2H. Из центра проведем отрезки к концам хорды. Получим равнобедренный треугольник,т.к. радиусы окружности равны,а значит отрезок соединяющий хорду с центром основания конуса является и высотой и медианой. От сюда следует,что данный отрезок делит полученный равнобедренный треугольник на два равных прямоугольных треугольников,а так же делит хорду попалам, и ее половина равна 4корень из2. Тогда по теореме Пифагора найдем радиус:R= V16+32= V48=4V3. Образующая радиус и высота конуса образуют прямоугольный треугольник. Из этого треугольника найдем высоту. Н=R*tg60=4V3*V3=12см. Теперь найдем объем: V=1/3*п*48*12=192п см^3
8) Объем конуса равен: V=1/3пR^2H. Из центра проведем отрезки к концам хорды. Получим равнобедренный треугольник,т.к. радиусы окружности равны,а значит отрезок соединяющий хорду с центром основания конуса является и высотой и медианой. От сюда следует,что данный отрезок делит полученный равнобедренный треугольник на два равных прямоугольных треугольников,а так же делит хорду попалам, и ее половина равна 4корень из2. Тогда по теореме Пифагора найдем радиус:R= V16+32= V48=4V3. Образующая радиус и высота конуса образуют прямоугольный треугольник. Из этого треугольника найдем высоту. Н=R*tg60=4V3*V3=12см. Теперь найдем объем: V=1/3*п*48*12=192п см^3
100√2
Объяснение:
РА=2r=2*5=10 высота трапеции.
МА=АР
Теорема Пифагора
МР=√(РА²+МА²)=√(10²+10²)=10√2
МР=KN=10√2
(PK+MN)=(PM+KN); свойство трапеции в которую вписана окружность.
РК+МN=2*PM=2*10√2=20√2
S=PA(PK+MN)/2=10*20√2/2=100√2